MCS 275 Spring 2023 Homework 8 Solutions¶
- Course Instructor: Emily Dumas
- Contributors to this document: Emily Dumas, Johnny Joyce
Instructions:¶
- Complete the problems below, which ask you to write Python scripts.
- Upload your python code directly to gradescope, i.e. upload the
.pyfiles containing your work.
Deadline¶
This homework assignment must be submitted in Gradescope by Noon central time on Tuesday March 7, 2023.
Collaboration¶
Collaboration is prohibited, and you may only access resources (books, online, etc.) listed below.
Content¶
This assignment is about trees.
Resources you may consult¶
Most relevant:
- Worksheet 8 Solutions
- Lecture 16 - Trees
- Lecture 17 - BST
- Lecture 18 - Traversals
- Chapter 7 of Miller and Ranum
- trees.py
- treevis.py
- treeutil.py
- treeutil documentation
- Sample programs
- Downey's book
- MCS 260 course materials from Fall 2021:
Less likely to be relevant, but also allowed:
- Any other lecture of MCS 275 spring 2023.
- Python tour
- Slides from any lecture of my most recent MCS 260 course MCS 260, Fall 2021.
- Any lecture video posted on our course Blackboard site
- Downey's book
- Any other textbook listed on the course blackboard site under "Textbooks"
Point distribution¶
This homework assignment has 2 problems, numbered 2 and 3. The grading breakdown is:
| Points | Item |
|---|---|
| 3 | Autograder |
| 6 | Problem 2 |
| 6 | Problem 3 |
| 15 | Total |
The part marked "autograder" reflects points assigned to your submission based on some simple automated checks for Python syntax, etc. The result of these checks is shown immediately after you submit.
What to do if you're stuck¶
Ask your instructor or TA a question by email, in office hours, or on discord.
Problem 2: Common ancestor¶
If x and y are two nodes of the same binary tree (as Node objects), then the root node is an ancestor of both of them (or is equal to one or both of them). So we see that any two nodes in a binary tree have a common ancestor.
Furthermore, any two nodes have a unique lowest common ancestor, i.e. the node a that is a common ancestor of both x and y, and such that no child of a is an ancestor of both x and y. Another way to describe a is that if you take the path in the tree that starts at x and ends at y, then a is the node on that path that is closest to the root. (And it's possible that a might be equal to x or to y, if one of x and y is an ancestor of the other.)
Write a function lowest_common_ancestor(x,y) that takes two Node objects x and y and returns their lowest common ancestor (another Node object). If there is no common ancestor (i.e. if x and y lie in different trees), return None.
Submit this function in a file hwk8prob2.py.
Solution¶
This solution uses a helper function ancestors (which is the same as in the example solution for worksheet 8, problem 1). This returns a list of all ancestors of a given node, starting with the node itself, then its parent, then its parent's parent, etc.
def ancestors(x):
"""
Given node, returns list containing its parent, its parent's parent, etc.
"""
L = [x]
while L[-1].parent != None: # While we can find a parent of the most recently-found parent
L.append(L[-1].parent) # Put parent into the list
return L
def lowest_common_ancestor(x,y):
"""
Given nodes `x` and `y`, returns common ancestor of x, y that has shortest distance to x and y
"""
# Pre-compute ancestors for each node (so we don't have to call ancestors() many times in a loop)
ancestors_x = ancestors(x)
ancestors_y = ancestors(y)
# Since ancestors are in order, the first match we find must be the lowest common ancestor
for node in ancestors_x:
if node in ancestors_y:
return node
# If no common ancestor is found, return None
return None
Problem 3: Ideal BST insert order¶
A binary tree with $(2^n-1)$ nodes can be "perfect" or "full" in the sense that it has as many nodes as possible for its depth. Here are some pictures of full binary trees:
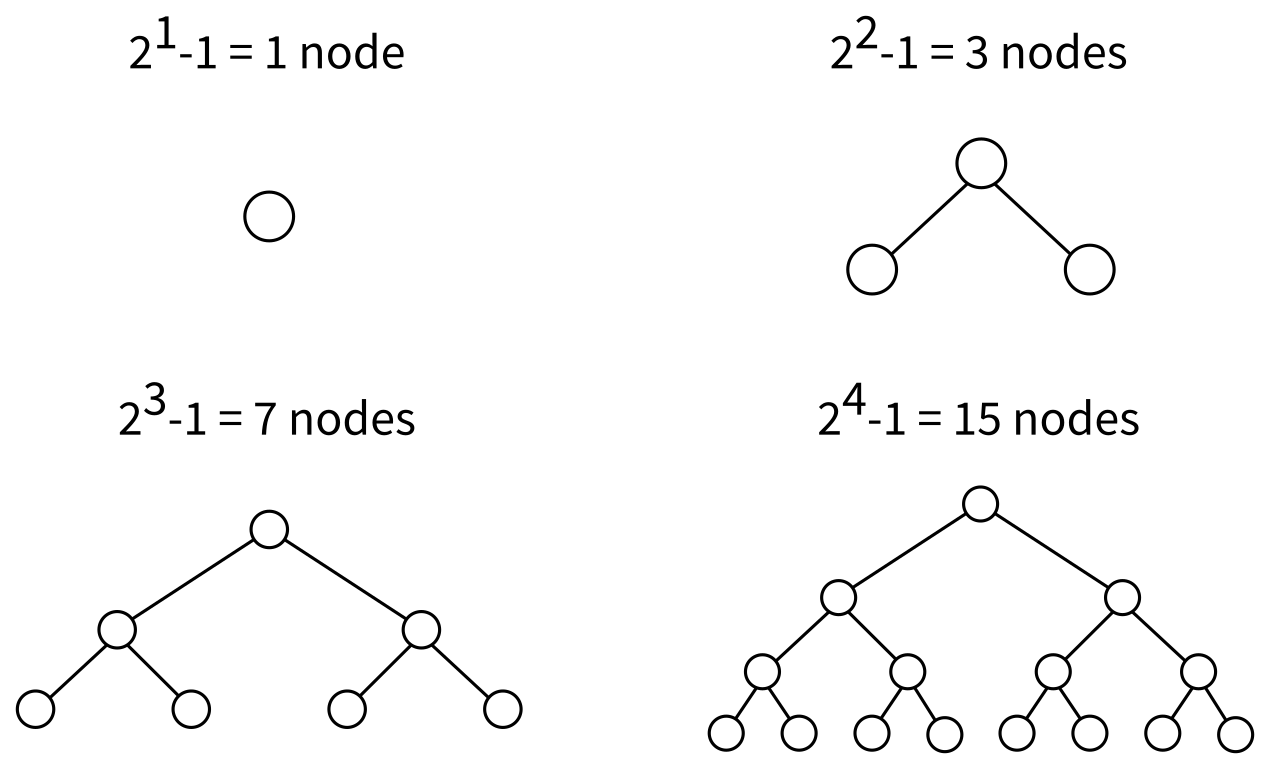
Now suppose we insert the integers $1$, $2$, ... $2^n-1$ into a binary search tree. We might get a full tree, or might not, depending on the order:
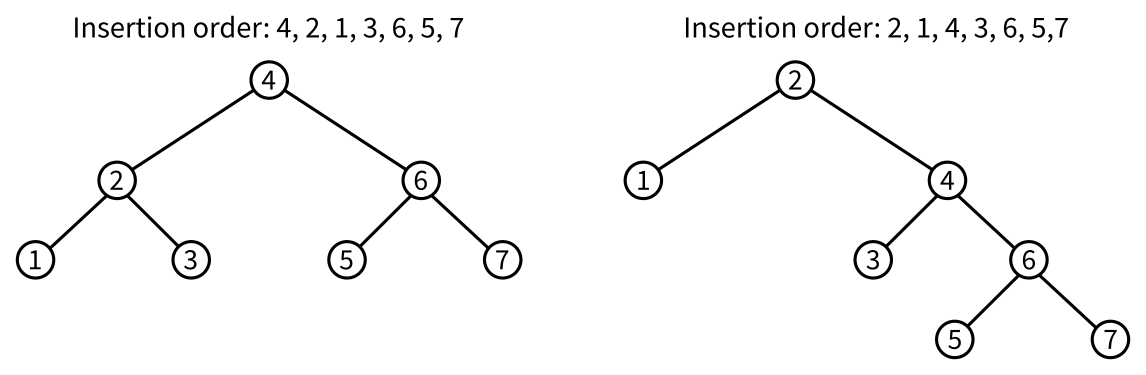
Write a function ideal_insert_order(n) that returns a list containing the integers from $1$ to $2^n-1$ (inclusive) in an order so that inserting them into a BST in that order results in a full tree.
For example, ideal_insert_order(3) might return [4,2,1,3,6,5,7]. (There are many other possible correct answers. But for example returning [1,2,3,4,5,6,7] would be wrong: Inserting in that order doesn't give a full tree.)
It's important your function works for any n (subject only to limits imposed by time, memory, and/or recursion depth) and is not hard-coded to work only for a single value or a few of them.
Submit this function in a file hwk8prob3.py.
Solutions¶
There are many ways to solve this question, so a few different versions are given:
ideal_insert_order1is a recursive implementation inspired by mergesort.ideal_insert_order2is a recursive implementation that makes a list following a certain pattern, which ensures it is an ideal insert order.ideal_insert_order3is a solution that creates a tree with blank nodes, fills it in as a BST, then performs a preorder traversal.ideal_insert_order4solves the question in a single statement using possibly-surprising methods.
Solutions 1 and 2 are the most accessible and are rather similar to one another. Solution 3 is the most direct (but longest). Solution 4 can be an interesting challenge to think about.
The final cell in this notebook also contains some code that can be used to verify that the solutions work as intended.
Solution 1 (recursive, like mergesort)¶
def ideal_insert_order1(n, keys = None):
"""
An approach inspired by mergesort. Initialize a list of keys called `keys`. At
each step take the middle element of `keys` and put it in a list `L`. Then extend
L by making recursive calls on everything to the left of L and everything to the
right.
"""
if keys is None:
keys = list(range(1, 2**n))
if len(keys) <= 1: # Base case
return keys
middle = len(keys)//2
L = [keys[middle]] # Insert the "middle" key
# Split the list down the middle and make a recursive call on each side
L += ideal_insert_order1(n, keys[:middle])
L += ideal_insert_order1(n, keys[middle+1:])
return L
Solution 2 (Recursive, based on a pattern in the sequence)¶
Here's a solution you might develop if you notice that the ideal insert order 4,2,1,3,6,5,7 begins with a power of two, and the rest of it consists of two parts 2,1,3 and 6,5,7 that differ by adding a constant (6,5,7 is obtained from 2,1,3 by adding 4 to each term).
# The most accessible recursive solution based on
# recognizing a pattern in ideal insert orders:
def ideal_insert_order2(n):
"""
Find order of insertion for integers 1...2**n-1 that results in a full
binary tree. Do so by making a list of those integers where the first
element of the list is the median, and where dividing the rest into two
halves `A` and `B` gives:
* Every element of `A` is less than the median
* Every element of `B` is greater than the median
* All the conditions in this list hold for `A`
* All the conditions in this list hold for `B`
This ensures that when the first element is used as the root, all of `A`
ends up in the left subtree and all of `B` ends up in the right subtree. In
particular the left and right subtrees contain the same number of elements.
That this is recursively true at each stage (with each subtree having 2**k-1
elements for some k) ensures the resulting tree is full.
"""
if n == 1:
return [1]
L = ideal_insert_order2(n - 1)
return [2 * L[0]] + L + [2 * L[0] + x for x in L]
# power of two-^ part part shifted by constant
Solution 3 (most direct solution: make a blank tree and fill it in)¶
This solution being "most direct" means it applies the definition of an ideal insert order in the most straightforward way. It makes a full tree, fills it with values, then traverses in preorder to determine an insert sequence that would give that tree.
This ends up being a longer solution, but completely valid.
from trees import Node
def depth(T):
"""
Depth of a binary tree (in edges). Could use the method requested in
worksheet 8 instead, if present.
"""
if T == None:
# returning -1 here means we cancel count of edge
# that leads to an absent child.
return -1
return 1 + max(depth(T.left), depth(T.right))
def blank_full_tree(d, parent=None):
"""
Create a full binary tree of depth `d`. If given, `parent` sets the parent
of the root node of that tree. Returns the root node.
"""
if d < 0:
return None
n = Node(parent=parent)
n.left = blank_full_tree(d - 1, parent=n)
n.right = blank_full_tree(d - 1, parent=n)
return n
def inorder_nodes(T):
"""
Do an inorder traversal of binary tree `T` and return a list of node objects
in the order visited. This is very similar to `Node.inorder` except that it
returns the nodes themselves rather than just the keys.
"""
if T == None:
return []
return inorder_nodes(T.left) + [T] + inorder_nodes(T.right)
def ideal_insert_order3(n):
"""
Find order of insertion for integers 1...2**n-1 that results in a full
binary tree. Do so by making a full tree that has no keys (all are None),
then traversing it inorder and adding keys that are ascending integers as we
go. Then the list of keys seen in a preorder traversal will provide a way to
duplicate the tree, i.e. an ideal insertion order.
"""
# Make an full tree with all keys `None`
T = blank_full_tree(n - 1)
# Fill it with integers 1..2**n-1 in way so that
# it is a valid BST (i.e. preorder = ascending order)
for i, node in enumerate(inorder_nodes(T)):
node.key = i + 1
N = 2 ** n - 1
assert i + 1 == N # check that we had the expected number of nodes!
# Now the preorder is an insert order that will reproduce the
# tree!
return T.preorder()
Solution 4 (Challenging: sort by binary representation)¶
Fun puzzle: Show that this solution really works!
def ideal_insert_order4(n):
"""
Find order of insertion for integers 1...2**n-1 that results in a full
binary tree. It turns out that one such order is obtained by the following:
* List all the integers (e.g. 1,2,3,4,5,6,7)
* Sort by the number of `1` bits when the number is represented in binary (low to high)
e.g. 1=0b001, 2=0b010, 4=0b001, 3=0b110, 5=0b101, 6=0b011, 7=0b111
* Within numbers with the same `1`-bit count, sort by the corresponding
numeric value, but in decreasing order.
e.g. [#1bits = 1] 4=0b100, 2=0b010, 1=0b001,
[#1bits = 2] 6=0b110, 5=0b101, 3=0b011,
[#1bits = 3] 7=0b111
* Return the associated order of the integers e.g. 4, 2, 1, 6, 5, 3, 7
We don't mean to imply that this is an easily discoverable characterization,
nor that it's within the scope of MCS 275. But when combined with some
built-in constructions (like binary conversion, anonymous functions,
range(), sorting with custom order, etc.) it yields a solution in one
statement. That's why we choose to show it here.
HOWEVER, note this doesn't return the same list as `ideal_insert_order1` and
`ideal_insert_order2`. There are many possible ideal insert orders, as the
assignment explains.
"""
return sorted(
range(1, 2 ** n), # integers 1..2**n-1
key=lambda k: ( # sort by tuple
bin(k).count("1"), # count 1-bits in binary
-k, # secondary factor: sort by numeric value, decreasing
),
)
Code for testing:¶
import trees
import treevis
# List of solutions we're checking
iio_fns = [
ideal_insert_order1,
ideal_insert_order2,
ideal_insert_order3,
ideal_insert_order4
]
n = 4
for iio in iio_fns:
print("TESTING SOLUTION:",iio.__name__)
T = trees.BST()
for node in ideal_insert_order1(n):
T.insert(node) # Insert nodes in the order given by our function
print("The nodes we want to insert are: {}".format(list(range(1, 2**n))))
print("The resulting tree is:")
treevis.treeprint(T)
print()
Revision history¶
- 2023-03-03 Initial publication