Random Chords Applet

Previously, the Random Chords applet was embedded in this page. Modern browsers do not support Java applets, so to use the applet you need to download it.

Download

• RandomChord.jar (Executable JAR)
• RandomChord.tar.gz (Source code)

Running the applet

On most Linux distributions with a java interpreter installed, you can run the applet with the command:

java -jar RandomChord.jar

On other platforms, the steps necessary to run an applet from a JAR will vary.

Discussion

Quick-start instructions: Press Add Chords many times and watch the show.

This applet demonstrates a result from the paper:

• Distribution of intersection lengths of a random geodesic with a geodesic lamination by Martin Bridgeman and Emily Dumas, to appear in Ergodic Theory Dynam. Systems.

Given an ideal triangle T in the hyperbolic plane H², we consider the function L: T¹T → R₊ (where T¹T is the unit tangent bundle of T) whose value at a vector v is the hyperbolic length of the geodesic chord of T containing v. There is a natural probability measure μ on the unit tangent bundle of T, and we show that the pushforward of μ by L has differential expression

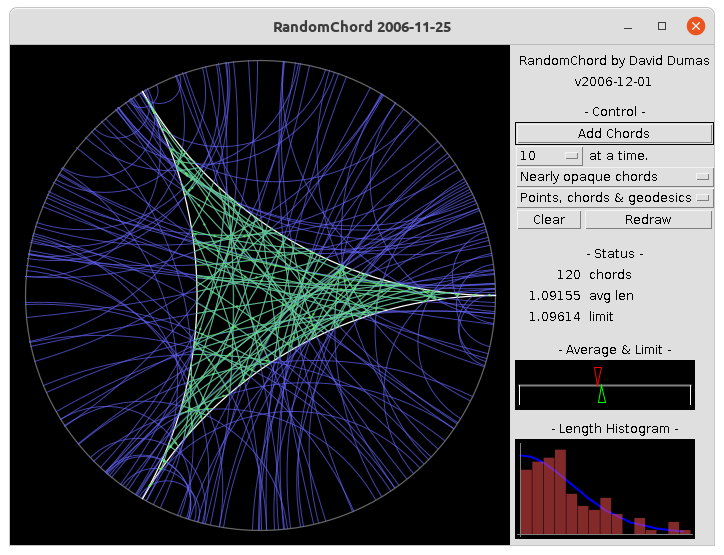
In particular, the expected length of the chord containing a randomly chosen point and unit tangent vector is (9/π²)ζ(3) = 1.096144454... . In the applet, one can observe the convergence of the sample distribution of a large but finite set of chord lengths to this limiting continuous distribution. The main display at left shows the basepoints and chords, while the displays at right show the mean length (and an interval of width 4σ/√n centered at the mean) and a 15-bin histogram of the lengths (compared to the theoretical distribution curve).

Note that the convergence is not particularly fast; you should try 5000 to 10000 chords to see convincing results. The java drawing functions are also somewhat slow, so a complete redraw of this many chords (e.g. if you change from transparent to opaque, or from complete geodesics to chords, etc.) will take quite a while. Adding additional chords should remain relatively quick, however.

In the paper, the distribution of chord lengths is used to derive further results about the intersections between a generic geodesic ray on a compact hyperbolic surface and a maximal geodesic lamination.