

by Emily Dumas and François Guéritaud




Thurston's embedding was introduced in the 1986 paper Minimal stretch maps between hyperbolic surfaces. Thurston showed that for any hyperbolic structure X on the surface, the map which takes a class [λ] in PML(S) to the covector dX(log Lλ) embeds PML(S) as the boundary of a convex neighborhood of the origin in the cotangent space TX*Teich(S). Here Lλ : Teich(S) → R is the hyperbolic length function.
For visualization purposes it is natural to consider cases in which the real dimension of the cotangent space of Teichmüller space is as small as possible. However, for closed orientable surfaces, this real dimension is at least six. We therefore consider non-orientable surfaces and surfaces with punctures.
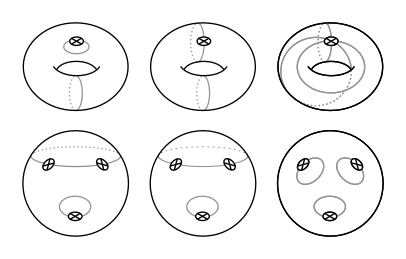
There are three types of simple closed curves on N3:
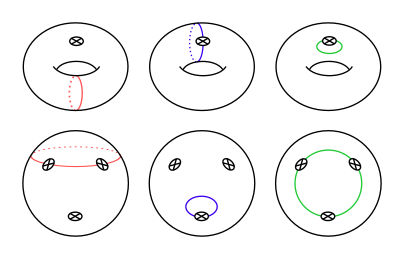
A multi-curve on N3 is either the union of the two curves in a dual pair, a two-sided curve and the special one-sided curve, or the union of two or three disjoint one-sided curves. Examples are shown below.
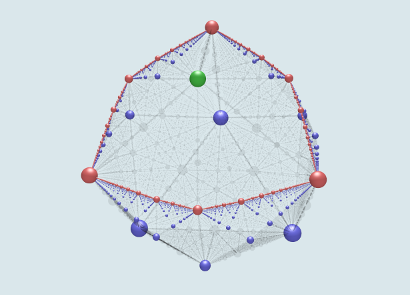
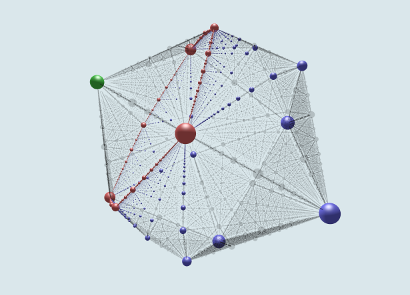
To make a picture of Thurston's embedding, we mark the point in TX*Teich(N3)=R3 corresponding to a simple closed curve with a sphere whose radius is inversely proportional to the hyperbolic length of the corresponding geodesic. The spheres are colored according to the topological type of the associated curve as indicated above.
In the resulting pictures (see below), we see that the two-sided simple curves on N3 give a dense subset of a Jordan curve in two-dimensional sphere PML(N3). This equator curve is the projective measured lamination space PML(S1,1), which naturally embeds in PML(N3) through the torus picture described above. The one-sided curves in N3 dual to these two-sided simple curves accumulate on the equator from one side (i.e. they lie in one "hemisphere"). The other open hemisphere of PML(N3)) contains only one simple curve: the special one-sided curve.
As before, the Teichmüller space has real dimension three, and there are one-sided simple curves, two-sided simple curves, and multi-curves. While PML(N1,3) is again homeomorphic a 2-sphere, it was shown by M. Scharlemann (see The complex of curves on non-orientable surfaces. J. London Math. Soc. 25 (1982) 171-184) that in this case the closure of the set of two-sided simple curves is an Apollonian gasket. In contrast, each one-sided curve is an isolated point in the set of simple curves; in fact, there is a single one-sided simple curve in each connected component of the complement of the gasket.
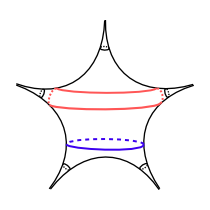
We use the "pentagonal" hyperbolic structure as the base point X for the Thurston embedding. This is the hyperbolic structure obtained by doubling a regular ideal pentagon across its boundary. We identify the tangent space TXTeich(S0,5) with R4 using a basis obtained from infinitesimal earthquake deformations along simple closed geodesics. In order to produce a symmetric picture, some care must be taken to choose a basis respecting the symmetry of the hyperbolic structure X. Specifically, we start with the blue and red geodesics shown below:
We therefore choose a basis {v1,v2,v3, v4} for the tangent space in which the blue earthquake vectors lie in the span of {v1,v2} and the red earthquake vectors lie in the span of {v3,v4}. Moreover the basis is chosen so that either collection forms the vertex set of a regular pentagon inscribed in the unit circle of its corresponding plane (considering the vectors vi to be orthonormal for the purposes of this geometric description).
After stereographic projection, we proceed as before, marking each of the resulting points with a sphere whose radius is inversely proportional to the hyperbolic length of the corresponding geodesic. Note that the sizes of the spheres are computed after stereographic projection: The length of the curve determines the Euclidean radius of the sphere drawn R3, rather than a spherical radius in S3. (While using spherical radii would seem more natural, the resulting pictures are cluttered and confusing. The few large spheres near infinity dominate the view and make it difficult to see the local structure near the origin.)
Despite the inherent distortion when using stereographic projection to visualize the boundary of this four-dimensional convex set, the intricate structure of PML and of the complex of curves is once again evident. Families of simple closed curves that lie in various four-punctured-sphere subsurfaces appear as a network of thin "filaments". Dehn twist families are seen approaching short curves from many directions.
For better quality: Download the video file – 51MB, 8000kbit/s h.264 MP4
This video is released under the CC-BY 4.0 license.
For better quality: Download the video file – 78MB, 8000kbit/s h.264 MP4
This video is released under the CC-BY 4.0 license.
The poster is intended for printing on "ARCH D" size paper (24in x 36in or 610mm x 914mm).
Lists of words representing simple closed curves were generated by programs written in Python, by applying mapping class group elements to a set of "seed" words representing the different orbits. The visualizations shown above include 50,000 to 2,000,000 simple closed curves. The hyperbolic lengths and derivatives were then calculated by a finite difference method, resulting in data files representing Thurston's embedding.
A final set of Python programs handled stereographic projection, rotations, computing radii, and generating geometric primitives in the input format expected by the ray tracer POV-Ray. A separate template POV-Ray scene file set lighting, background, and texture parameters for the images and animations.
To create the videos, individual frame images were rendered with POV-Ray and then combined and encoded as h.264 video using FFmpeg. Rendering was the most time-consuming step in the process; each frame took between 5 and 30 minutes to render with a 3.7Ghz Intel Xeon E3-1290 V2 CPU.
This material is based upon work supported by the National Science Foundation. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author and do not necessarily reflect the views of the National Science Foundation.