Lecture 9

Recursion

MCS 275 Spring 2023
Emily Dumas

Lecture 9: Recursion

Reminders and announcements:

• Homework 4 due Tuesday at Noon
• Project 1 due next Friday, Feb 10, at 6pm

Recursion

In computer science, recursion refers to a method of solving a problem that depends on solving a smaller version of the same problem.

Usually, recursion involves a function calling itself.

Strategies using recursion

• Divide and conquer: A problem can be split into pieces; solutions for the pieces can be combined to the full solution.
• e.g. Mergesort
• "Decrease and conquer": Reduce a problem for a given input (e.g. n) to the answer for a slightly smaller input (e.g. n-1) and a bit of extra work.
• e.g. Factorial

Iteration

Recursive solutions are often contrasted with iterative solutions.

• Iterative: Loops and local variables keep track of all state (work to be done, work completed, next ...)
• Recursive: Arguments keep track of current state; return values send back results.

Recursive solutions can always be converted to iterative ones, often at the cost of more complex code.

Stop condition

A function that always calls itself will never finish!

Recursion must include some kind of stop condition—a case in which the function can directly return an answer instead of calling itself.

Today's examples

• Factorial
• Fibonacci numbers
• Paper folding sequence

Factorial

The classic first example of recursion, computing $$n! = n \times (n-1) \times \cdots \times 2 \times 1.$$

The argument to the function decreases with each subsequent call, so it eventually reaches the stop condition ($n \leq 1$).

Fibonacci

The Fibonacci numbers are defined by $$F_0=0,\; F_1=1,\; \text{and }F_n = F_{n-1} + F_{n-2}$$

So the sequence begins $0,1,1,2,3,5,8,13,...$

The definition immediately suggests a recursive implementation.

Paper folding sequence

• Start with a strip of paper
• Fold it in half n times, always in the same direction
• Unfold and read the in/out creases 0 and 1

Paper folding sequence

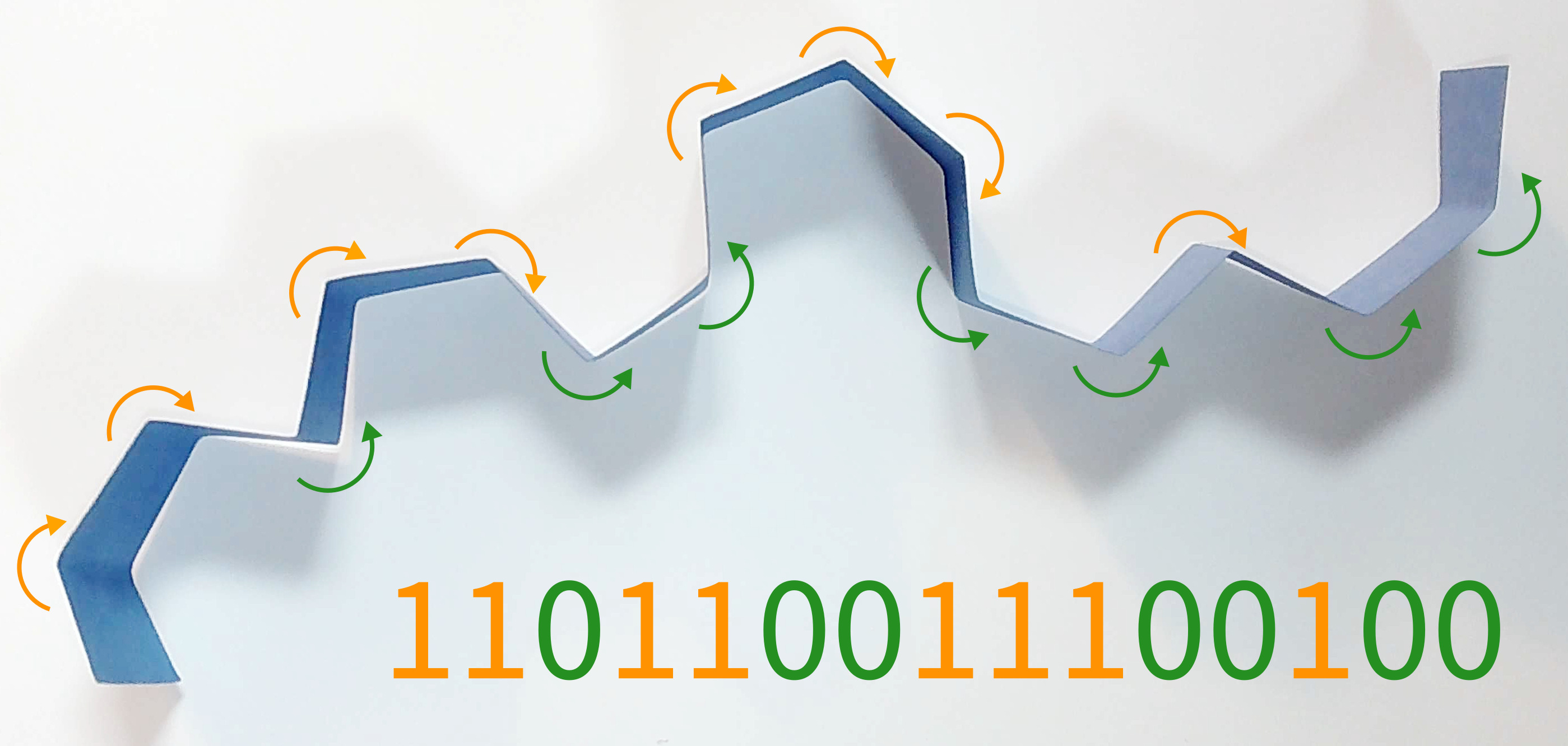
Paper folding sequence

Let's use $\oplus$ to mean concatenation of binary sequences, so $0110 \oplus 11 = 011011$.

If $A$ is a binary sequence, let $\bar{A}$ denote the sequence with $0$ and $1$ switched, e.g. $\overline{11101} = 00010$

Finally, let $A^r$ denote the sequence in opposite order, e.g. $10010^r = 01001$.

$$PFS(n) = PFS(n-1) \oplus 1 \oplus \overline{PFS(n-1)^r}$$

Limited recursion depth

Recursive functions are limited by a maximum call stack size. The call stack is a data structure that keeps track of function calls that are currently underway.

• Calling a function → pushing onto call stack
• Returning from a function → popping from call stack

Python imposes a limit to prevent the memory area used to store the call stack from running out (a stack overflow), which would abruptly stop the interpreter.

Iterative solutions

Let's write iterative versions of factorial, Fibonacci, and paper folding. (Or as many as time allows.)