Lecture 14
Recursion vs Iteration II
MCS 275 Spring 2022
Emily Dumas
Lecture 14: Recursion vs Iteration II
Course bulletins:
- Project 1 graded.
- Feedback survey open.
- Project 2 description coming Monday.
- Project 2 due 6pm CST Friday, February 25.
- Remember to check the recursion sample code.
Fibonacci timing
| n=35 | |
|---|---|
| recursive | 1.9s |
| iterative | <0.001s |
Measured on a 4.00Ghz Intel i7-6700K CPU (2015 release date) with Python 3.8.5
fib call graph
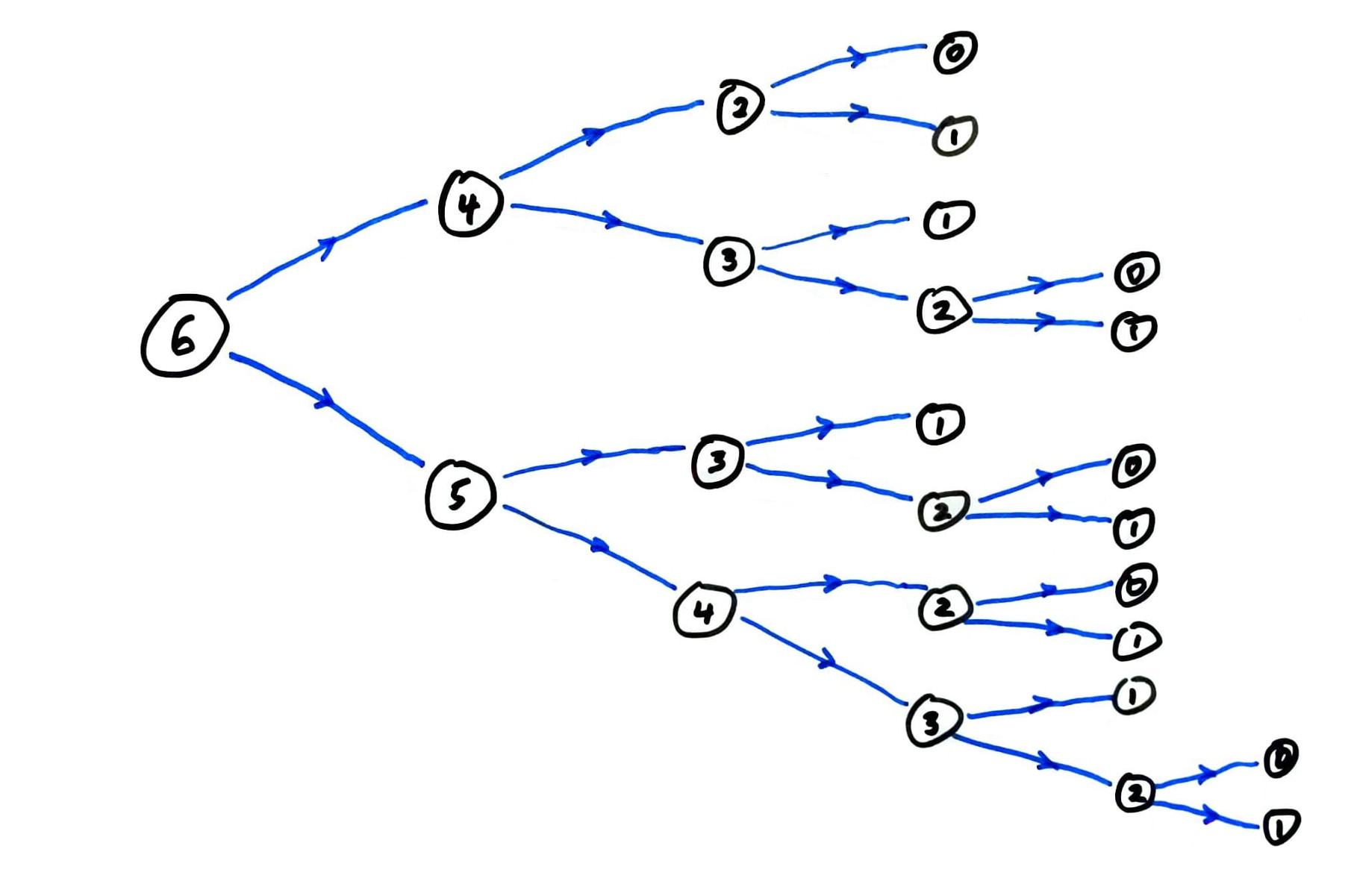
Most Fibonacci numbers are computed many times!
fib call graph
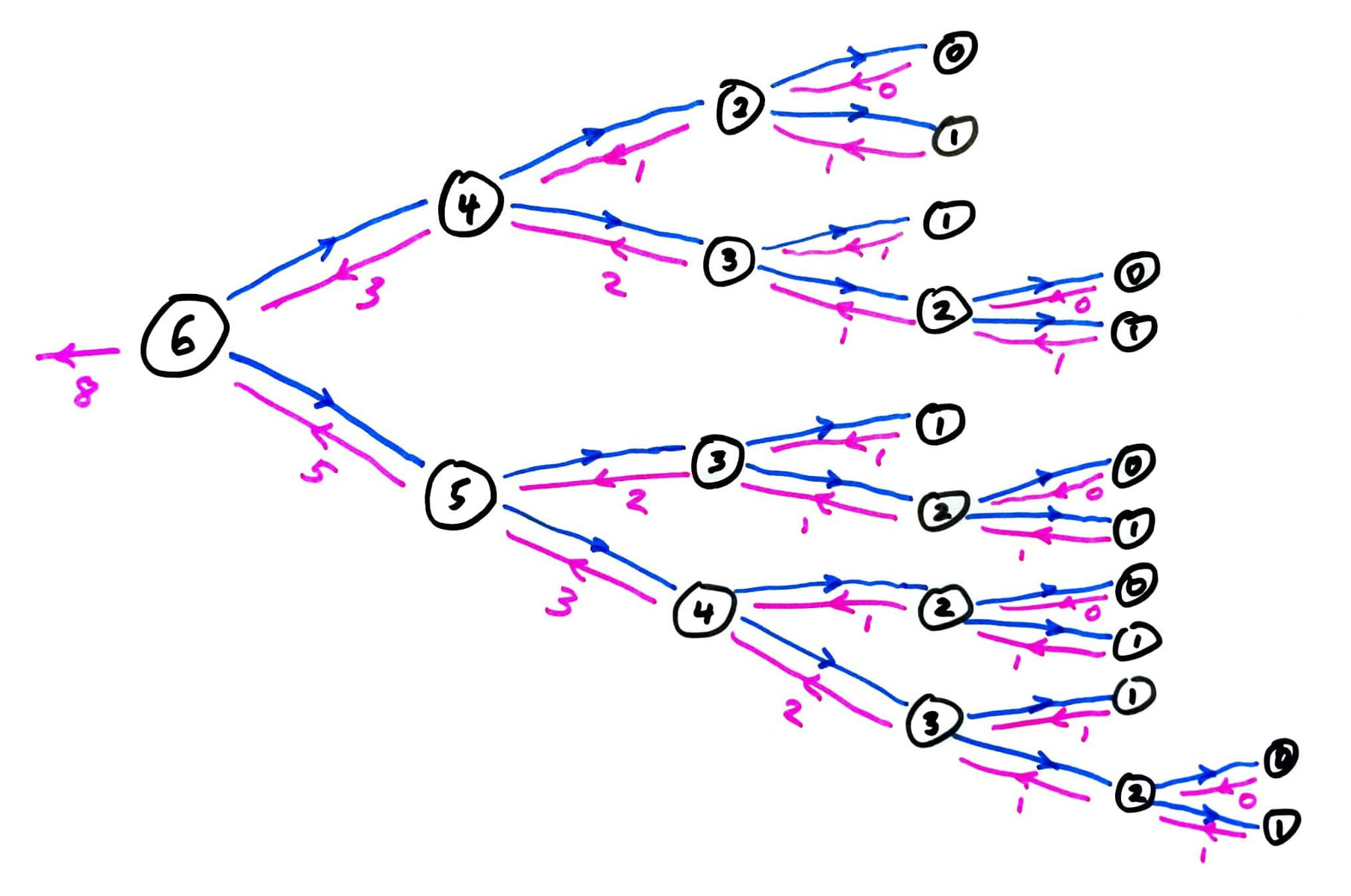
Most Fibonacci numbers are computed many times!
Memoization
fib computes the same terms over and over again.
Instead, let's store all previously computed results, and use the stored ones whenever possible.
This is called memoization. It only works for pure functions, i.e. those which always produce the same return value for any given argument values.
math.sin(...) is pure; random.random() is not.
Memoizing fib
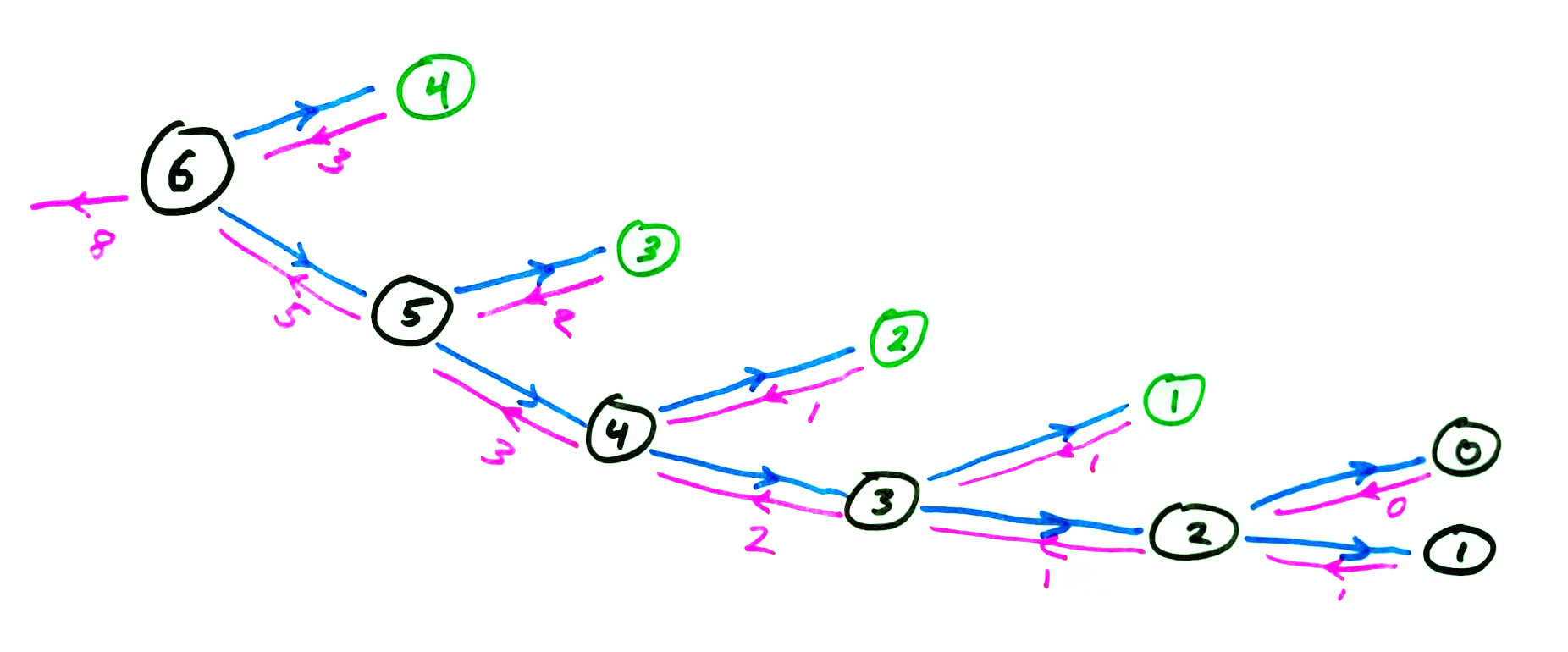
Let's add a simple memoization feature to our recursive fib function.
memoized fib call graph
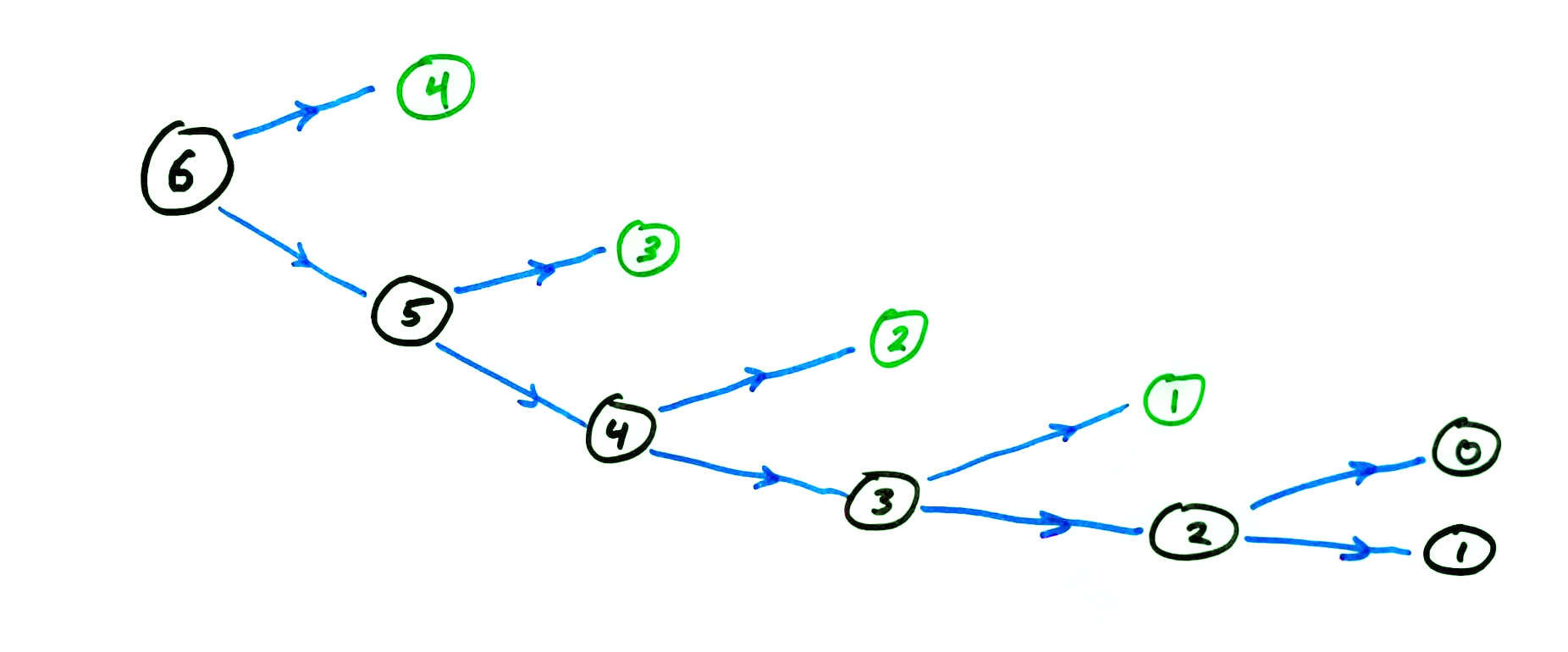
memoized fib call graph
Fibonacci timing summary
| n=35 | n=450 | |
|---|---|---|
| recursive | 1.9s | > age of universe |
| memoized recursive | <0.001s | 0.003s |
| iterative | <0.001s | 0.001s |
Measured on a 4.00Ghz Intel i7-6700K CPU (2015 release date) with Python 3.8.5
Memoization summary
Recursive functions with multiple self-calls often benefit from memoization.
Memoized version is conceptually similar to an iterative solution.
Memoization does not alleviate recursion depth limits.
Call counts
One way to measure the expense of a recursive function is to count how many times the function is called.
Let's do this for recursive fib.
| $n$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|---|
| calls | 1 | 1 | 3 | 5 | 9 | 15 | 25 | |
| $F_n$ | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 |
fib is called to compute fib(n). Then
$$T(0)=T(1)=1$$ and $$T(n) = T(n-1) + T(n-2) + 1.$$
Corollary: $T(n) = 2F_{n+1}-1$.
Proof of corollary: Let $S(n) = 2F_{n+1}-1$. Then $S(0)=S(1)=1$, and $$\begin{split}S(n) &= 2F_{n+1}-1 = 2(F_{n} + F_{n-1}) - 1\\ &= (2 F_n - 1) + (2 F_{n-1}-1) + 1\\ & = S(n-1) + S(n-2) + 1\end{split}$$ Therefore $S$ and $T$ have the same first two terms, and follow the same recursive definition based on the two previous terms.
Corollary: Every time we increase $n$ by 1, the naive recursive fib does $\approx61.8\%$ more work.
(The ratio $F_{n+1}/F_n$ approaches $\frac{1 + \sqrt{5}}{2} \approx 1.61803$.)
Recursion with backtracking

How do you solve a maze?
Recursion with backtracking

How do you solve a maze?
My guess at your mental algorithm:
- Try something (move around but don't return to anywhere you've visited).
- If you reach a dead end, go back a bit and reconsider which way to go at a recent intersection.
An algorithm that formalizes this is recursion with backtracking.
We make a function that takes:
- The maze
- The path so far
Its goal is to add one more step to the path, never backtracking, and call itself to finish the rest of the path.
But if it hits a dead end, it needs to notice that and backtrack.
Backtracking
Backtracking is implemented through the return value of a recursive call.
Recursive call may return:
- A solution, or
None, indicating that only dead ends were found.
depth_first_maze_solution:
Input: a maze and a path under consideration (partial progress toward solution).
- If the path is a solution, just return it.
- Otherwise, enumerate possible next steps that don't go backwards.
- For each of the possible next steps:
- Make a new path by adding this next step to the current one.
- Make a recursive call to attempt to complete this path to a solution.
- If recursive call returns a solution, we're done. Return it immediately.
- (If recursive call returns
None, continue the loop.)
- If we get to this point, every continuation of the path is a dead end. Return
None.
Depth first
This method is also called a depth first search for a path through the maze.
Here, depth first means that we always add a new step to the path before considering any other changes (e.g. going back and modifying an earlier step).
Maze coordinates

References
Same suggested references as Lecture 13.
Revision history
- 2021-02-11 Initial publication