MCS 275 Spring 2022 Project 3

• Course instructor: David Dumas

Instructions

Deadline is 6pm central time on Friday 18 March 2022.

Collaboration policy and academic honesty

This project must be completed individually. Seeking or giving aid on this assignment is prohibited; doing so constitutes academic misconduct which can have serious consequences. The only resources you are allowed to consult are the ones listed below. If you are unsure about whether something is allowed, ask. The course syllabus contains more information about the course and university policies regarding academic honesty.

Topic

This project focuses on building a tree-based data structure that has similarities to a binary search tree, but which stores points in the plane.

Resources you are allowed to consult

• Documents and videos posted to the course web page
• Any of the optional textbooks listed on the course web page

Ask if you are unsure whether a resource falls under one of these categories, or if you think I missed an essential resource.

What to do if you are stuck

Contact the instructor or your TA by email, in office hours, or on discord.

Get the updated plane.py

There's no "starter pack" for this project, but you will need to use the latest version of the module planefor working with vectors and points. The version in the course sample code repository has already been updated to have a few new features that will be important in this project. You should download it now, saving it in the directory where you'll work on project 3:

• plane.py

What to submit

Submit two files:

• pointtree.py
• builder.py

The rest of this document describes what goes in these two files.

Introduction

Binary search trees can use any ordered data type as a key. It is only required that any two keys compare as either > or < or ==. This makes binary search trees suitable for storing a collection of integers, floats, or strings, for example.

But what if you wanted to make a tree where the keys are points in the 2-dimensional plane $(x,y)$? There isn't a single preferred way to say that one point is "less than" another. Would you use the $x$ coordinate? The $y$ coordinate? Both, in some way? Thus, while you could use a binary search tree, it isn't a perfect fit.

Instead, there are a number of tree-based data structures that are specially adapted to storing points in the plane. In this project, you'll implement one of them.

Sectors and relative position

First, let's discuss the geometric idea we'll use in place of the operators < and > that appear in binary search trees.

Suppose you have a 2-dimensional vector $V = (v_x,v_y)$ that is not the zero vector. This is usually drawn as an arrow, like in the diagram below.

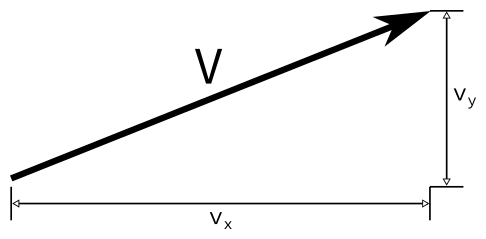
Such a vector has an angle $\theta$ that indicates how much you must rotate the positive x-axis in order for it to point in the same direction as $V$.

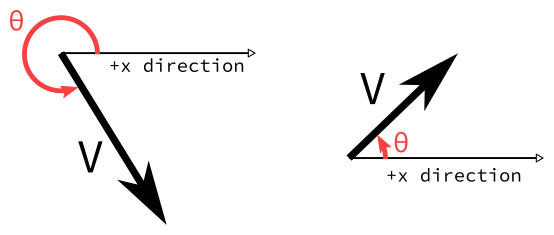
The angle can be measured in radians ($0 \leq \theta < 2 \pi$) or in degrees ($0^\circ \leq \theta < 360^\circ$). Note we use a convention where the angle is always positive.

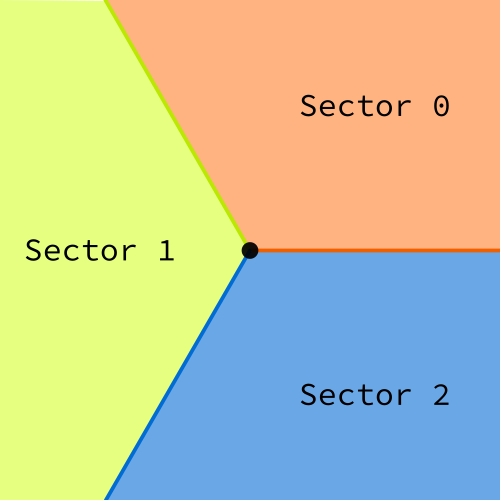
For this project, we won't care so much about the exact angle of a vector, but will instead look at which third of the circle of directions it lies in. We define:

• Vector $V$ is in sector 0 if its angle $\theta$ satisfies $0 \leq \theta < \frac{2\pi}{3}$, or equivalently $0^\circ \leq \theta < 120^\circ$
• Vector $V$ is in sector 1 if its angle $\theta$ satisfies $\frac{2\pi}{3} \leq \theta < \frac{4\pi}{3}$, or equivalently $120^\circ \leq \theta < 240^\circ$
• Vector $V$ is in sector 2 if its angle $\theta$ satisfies $\frac{4\pi}{3} \leq \theta < 2\pi$, or equivalently $240^\circ \leq \theta < 360^\circ$

In other words, the vectors in each sector 0,1,2 form a third of the plane. These sectors are shown below. Note that each sector is "half open": The boundary ray that is most clockwise for a given sector is part of the sector, the other boundary ray is not. This is shown in the figure using color coding: The orange ray is part of the orange sector, etc..

Now, if you have a point $P$ that you think of as your current location, and another point $Q$ (not equal to $P$), you can form the vector $Q-P$ that describes the direction you must move from $P$ to get to $Q$. Then, you can ask which sector the vector $Q-P$ lies in, and the answer can be thought of as indicating roughly where $Q$ sits relative to $P$. Specifically, we define:

• Point $Q$ is in sector 0 of point $P$ if the vector $Q-P$ is in sector 0.
• Point $Q$ is in sector 1 of point $P$ if the vector $Q-P$ is in sector 1.
• Point $Q$ is in sector 2 of point $P$ if the vector $Q-P$ is in sector 2.

(Notice we defined what it means for a vector to be in a sector earlier, and the new part here is that we're defining what it means for one point to lie in a sector of another point.)

So starting from any point $P$, you can classify the other point $Q$ as lying in sector 0, 1, or 2 of $P$. This is analogous to the way you can start with a real number $x$ and classify another real number $y$ as lying to the right of $x$ or left of $x$. Instead of having two possible answers about the relative position (left, right), we have three possible answers (sector 0, sector 1, sector 2). We've chosen to divide the plane into three sectors, but of course a similar idea could be pursued for quarters of the plane, fifths of the plane, etc..

An example

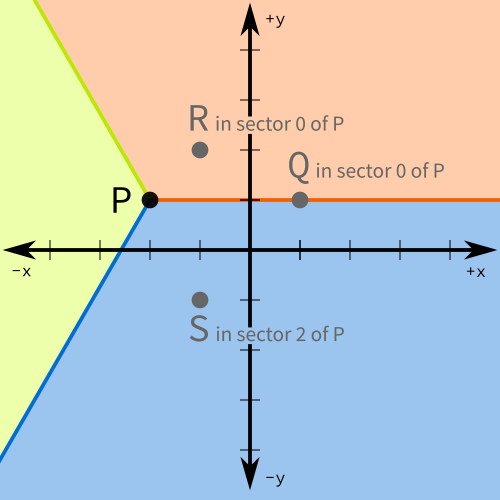
The sectors based at the point $P = (-2,1)$ are shown below. In this diagram, you see that $Q=(1,1)$ and $R=(-1,2)$ lie in sector 0 of P, and $S=(-1,-1)$ lies in sector $2$ of $P$.

In code

You don't need to do any manual sector or angle calculations. Instead, I've updated the module plane so that it can compute the sector or angle of a vector, and the sector of one point that contains another.

Specifically, the following methods have been added:

• Vector2.angle() - returns the angle of the vector, in radians. If the vector is zero, raises ValueError

• Vector2.sector() - returns an integer 0, 1, or 2, indicating which sector the vector lies in. If the vector is zero, raises ValueError

• Point2.sector_of(Q) - When called as a method of point P, and given an argument Q, returns the sector of the vector Q-P. So P.sector_of(Q) returns 0, 1, or 2, depending on which sector of point P contains Q.

Here is a demonstration:

import plane

V = plane.Vector2(1,1)
W = plane.Vector2(-3,1)
print(V,"is in sector",V.sector())
print(W,"is in sector",W.sector())
print()

P = plane.Point2(-2,1)
Q = plane.Point2(1,1)
R = plane.Point2(-1,2)
S = plane.Point2(-1,-1)

for other in [Q,R,S]:
    print(other,"is in sector",P.sector_of(other),"of",P)

Vector2(1,1) is in sector 0
Vector2(-3,1) is in sector 1

Point2(1,1) is in sector 0 of Point2(-2,1)
Point2(-1,2) is in sector 0 of Point2(-2,1)
Point2(-1,-1) is in sector 2 of Point2(-2,1)

The data structure: Trisection Search Trees (TSTs)

Definition

A trisection search tree or TST is a data structure consisting of a tree of nodes. Each node has a key which is a point in the plane (a Point2 object from module plane). Each node has three children, called child 0, child 1, and child 2, each of which is either another node or None. The nodes in a TST are required to satisfy the following conditions:

• A node is only allowed to have key None if it is the only node in the entire tree; this represents an empty TST.
• If a node $x$ has key $P$, then the keys of child 0 and its descendants are all in sector 0 of point $P$
• If a node $x$ has key $P$, then the keys of child 1 and its descendants are all in sector 1 of point $P$
• If a node $x$ has key $P$, then the keys of child 2 and its descendants are all in sector 2 of point $P$

In other words, when you move from a node to child $i$, you know that all the keys you see from now on will be in sector $i$ of the node you were previously on.

This is a direct analogue of a binary search tree, but instead of "left" and "right" we have "child 0", "child 1", "child 2".

Example

Here's a concrete example. Consider the following arrangement of points in the plane:

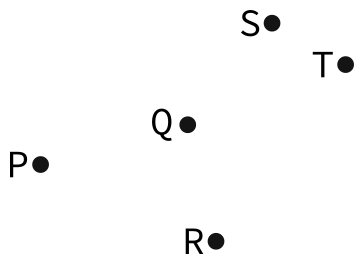
There are many different TST structures that can store this set of points. As with BST, the tree you get will depend on the insertion order of the points. Here is an example of one such tree that you might get:

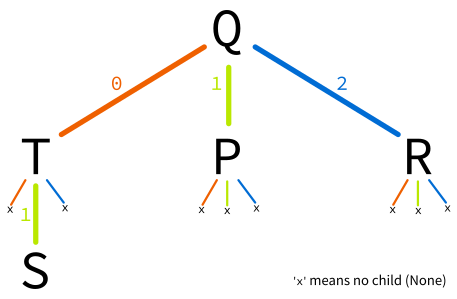
In this diagram, edges indicate children, with a label showing the number of the child. In the Python implementation you'll develop, the three children are stored in a list called child. So an edge from a node x to a child y labeled 2 means that y would be equal to x.child[2].

To see why this is a possible TST for that set of points, first consider the sectors based at the root, $Q$:

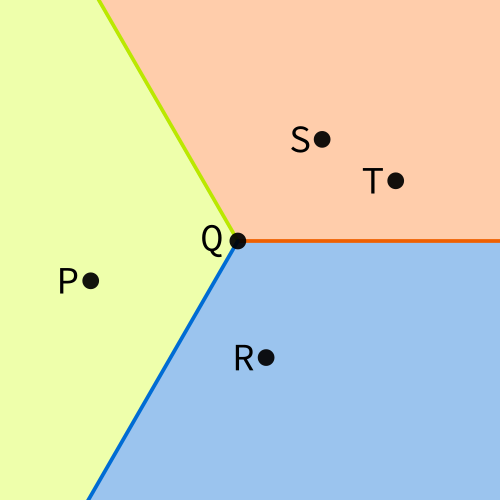
From this diagram we see:

• $S$ and $T$ lie in sector 0 of $Q$, so they must appear in the subtree of child 0 of $Q$
• $P$ lies in sector 1 of $Q$, so $P$ must appear in the subtree of child 1 of $Q$
• $R$ lies in sector 2 of $Q$, so $R$ must appear in the subtree of child 2 of $Q$

The tree shown above chose to make $T$ the child 0 of $Q$, and to make $S$ a child of $T$. To see which child of $T$ it should be, we can draw the sectors of $T$:

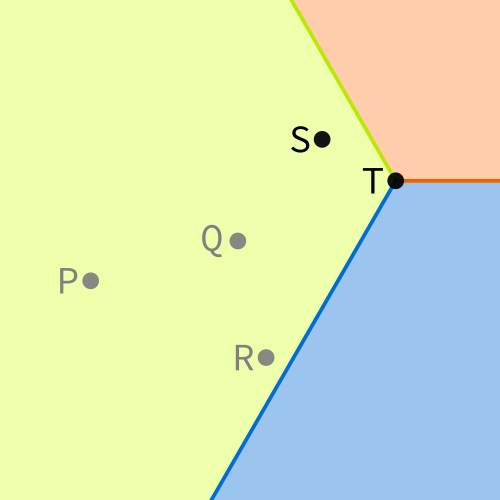
Note that we're focused on nodes $S$ and $T$ right now, so the others are grayed out in this diagram. We see that $S$ is in sector 1 of $T$, so $S$ must be child 1 of $T$ in this TST. That agrees with what we see in the tree diagram above. We have therefore checked that the tree shown above is a valid TST for this arrangement of points.

Optional topic: the region of a node

Not required for this project but of possible interest. In this example, $S$ was child 1 of $T$ and $T$ was child 0 of $Q$. What other points could be in that position? The answer is the intersection of two sectors: Sector 1 of $T$ and sector 0 of $Q$. This region is shaded in the diagram below.

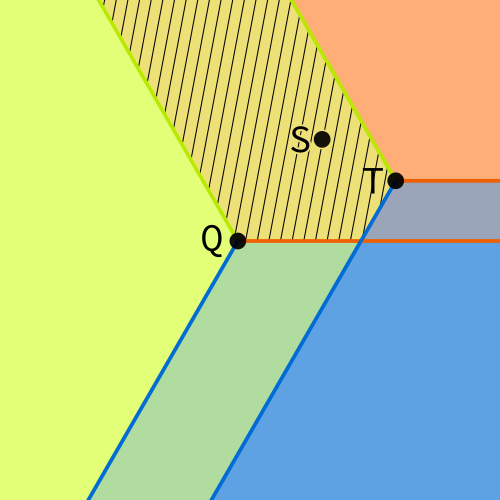
In general, as you descend into a TST, the region that you know will contain all subsequent points shrinks (each time being intersected with a certain sector of another point). This is similar to the way you gain more and more information about a node in a BST as you approach it from the root (e.g. it is larger than 5, less than 20, less than 18, larger than 16, ...). If you go deep enough into a TST (using an edge of each child type), the region of a node will become a bounded region, and in fact will be a hexagon!

Module pointtree

Finally, we come to the concrete description of the module you must write.

Write a module containing a single class TST that implements a trisection search tree that you can build, insert points into, search (find the node of a point if present), and query using the methods specified below. Save it in a file pointtree.py.

Class TST

instance attributes

• key, a Point2 object or None
• child, a list of length three. Its items are either None or TST objects.
• parent, a TST object or None

method __init__

Arguments:

• key, a Point2 object or None, with default value None

Behavior:

• Stores key in the attribute of the same name
• Initializes attribute child to be [None,None,None]
• Initializes attribtue parent to be None

Return value:

• None

method __str__

Arguments:

• None

Return value:

• A string in this exact format: TST(key=(1,3),children=[@@.]) Here, after key= it shows the x and y coordinates of the Point2 object, in parentheses, separated by a comma. If key is None then key=None would be shown instead. In the square brackets after children= it shows three characters that indicate the types of objects in list child, with None represented by . and any TST object represented by @. This provides a visual indicator of whether the node has children, and if so, which ones. The example string indicates that the node has a child 0 and a child 1, but does not have a child 2.

method __repr__

Same arguments and behavior as __str__.

method set_child

Arguments:

• i, an integer 0, 1, or 2
• node, a TST object or None

Behavior:

• If i is an integer other than 0, 1, or 2, raise ValueError. Otherwise:
• Set the item at index i in this node's attribute child to be node.
• If node is a TST object, set the parent of that object to be this node.

method get_child

Arguments:

• i, an integer 0, 1, or 2

Behavior:

• If i is an integer other than 0, 1, or 2, raise ValueError. Otherwise:
• Return the item at index i in attribute child

method insert

Arguments:

• p, a Point2 object

Behavior:

• If this node has key None, which is used to indicate an empty tree, just set the key to p and return. Otherwise, search through the TST and find a place where a new node with key p can be inserted while still obeying the TST conditions. After finding such a place, it creates a node (a TST object) with that key and makes it the appropriate child of an existing node in the tree.

Return value:

• None

method search

Arguments:

• p, a Point2 object

Return value:

• If the tree contains a node with key p, that node is returned. Otherwise, None is returned.

method __contains__

Arguments:

• p, a Point2 object

Return value:

• If the tree contains a node with key p, returns True. Otherwise, False is returned.

method __len__

Arguments:

• None

Return value:

• If the key of the current node is None, returns 0
• Otherwise, returns the total number of nodes in the tree (e.g. 1 if this node has no children)

method depth

Arguments:

• None

Return value:

• The maximum length, in edges, of a descending path through the tree starting from this node. (A nonnegative integer.)

method fill_fraction

Arguments:

• None

Return value:

• A float between 0 and 1 that is equal to the following fraction: $$ \frac{\left ( \text{ The number of nodes in this tree } \right )}{\left ( \text{ The maximum number of nodes that a TST of this depth could contain } \right ) } $$ Thus, this method will return 1 only for a tree in which every node has three children except the ones at maximum depth, which of course have no children.

Script builder.py

Note: The content of pointtree has the most weight in the grading of your project, so focus on correctness of that module before worrying too much about this program.

Write a program that imports your pointtree module and uses it as follows:

The program should expect one command line argument, the name of an existing text file. So, for example, it might be run as

python3 builder.py point_file.txt

The file whose name is given as a command line argument will have two integers on each line, separated by a single space. Here is an example of that format:

1 8
2 3
1 7
0 -2
-3 5

The program should open the given file, read the lines and interpret each line as a point, with the x coordinate given first and the y coordinate given second.

It should build a pointtree.TST object by inserting these points in the order they are given in the file.

Then, it should print statistics about the resulting tree in exactly the format shown below:

Built a TST with:
Root = (1,8)
Number of nodes = 5
Depth = 2
Fill fraction = 38%

This output sample corresponds to the actual values if the input file contains the 5 example points shown above (i.e. (1,8), (2,3), (1,7), (0,-2), and (-3,5)). Things to notice:

• The root is shown as (x,y) and not Point2(x,y)
• There is one space before and one space after each =
• The fill fraction shows an integer percentage. Use the value int(100*ff) where ff is the fill fraction (a float between 0.0 and 1.0).
• The maximum number of nodes that a TST of depth 2 can hold is 1+3+9=13, but this TST contains only 5 nodes, hence the fill fraction is 5/13, or about 0.384615384, which is displayed as 38%

For reference, in this example the final tree would end up looking like this:

     (1,8)
    /0 |1 \2
       |   \
       |    \
    (-3,5)  (2,3)
           /0 |1 \2
          /       \
       (1,7)     (0,-2)

The tree isn't shown in the output, though. I've shown it here so that the statistics in the output can be more easily checked.

IMPORTANT RULES YOUR CODE MUST FOLLOW

Your project must follow the 7 rules in the MCS 275 coding standards document. In addition:

• Use .sector() and .sector_of(...) whenever possible. If you have a vector V and need its sector, use V.sector(). If you have a point P and need to know which sector of P contains another point Q, use P.sector_of(Q). Do not do any angle or sector math yourself.

• Use get_child and set_child whenever possible. When you need to check children of an instance of class TST from code that runs outside the class, always use the methods provided for that purpose instead of direct access to the attribute .child.

How your project will be graded

Autograder: 60 points

The autograder tests your program and grades it based on its behavior. The following tests will be run:

1. Were files called pointtree.py and builder.py submitted? (5 points)
2. Does the Python interpreter accept the contents of pointtree.py and builder.py as valid Python code? (5 points)
3. Do the files pointtree.py and builder.py contain docstrings for all classes, functions, and methods? (5 points)
4. Can pointtree.py be imported without raising an exception, and does it contain a class called TST? (5 points)
5. Functional tests of the methods of class TST (35 points total, several tests of each method and of multiple methods in combination)
6. Functional tests of the program builder.py on various input data files (5 points total)

Manual review: 5 points

The usual review to check for code standards compliance, readability, other issues not detected by the autograder.

Final word: Submit before deadline

Plan your project work so that you can submit to the autograder as much before the deadline as possible. The first submission often has easily-fixed problems, and you want to allow yourself time to make those fixes.

Revision history

• 2022-03-02 Initial publication