Lecture 27

Julia sets

MCS 275 Spring 2021
Emily Dumas

Lecture 27: Julia sets

Course bulletins:

• Project 3 due 6:00pm CDT on Friday March 19.
• Some time today:
  • Project 3 autograder opens
  • Worksheet 10

Plan

• Finish numpy introduction notebook

• Julia sets notebook
• Julia sets notebook #2

Dynamics

Start with a function, e.g. $f(x) = x^2$, and a number, $a$.

Apply $f$ over and over again to get a sequence:

$a, f(a), f(f(a)), f(f(f(a))), ...$

This sequence $\{ f^{n}(a) \}_{n \geq 0}$ is the orbit of $a$ (under $f$). What can we say about it?

Let's start with a simple example, $f(x) = x^2$.

$2\to4\to16\to256 \to 65536\to\cdots$

$\frac{1}{2} \to \frac{1}{4} \to \frac{1}{16} \to \frac{1}{256} \to \frac{1}{65536} \to \cdots$

What happens for other starting points?

For real numbers, orbits under $f(x)=x^2$ are easy:

• If $|a|<1$, the orbit of $a$ converges to $0$
• If $|a|>1$, the orbit of $a$ goes to $\infty$
• If $|a|=1$ the orbit is bounded but doesn't go to $0$

For $f(x)=x^2$ with complex numbers, it's the same!

• If $|a|<1$, the orbit of $a$ converges to $0$
• If $|a|>1$, the orbit of $a$ goes to $\infty$
• If $|a|=1$ the orbit is bounded but doesn't go to $0$

$f(x)=x^2$

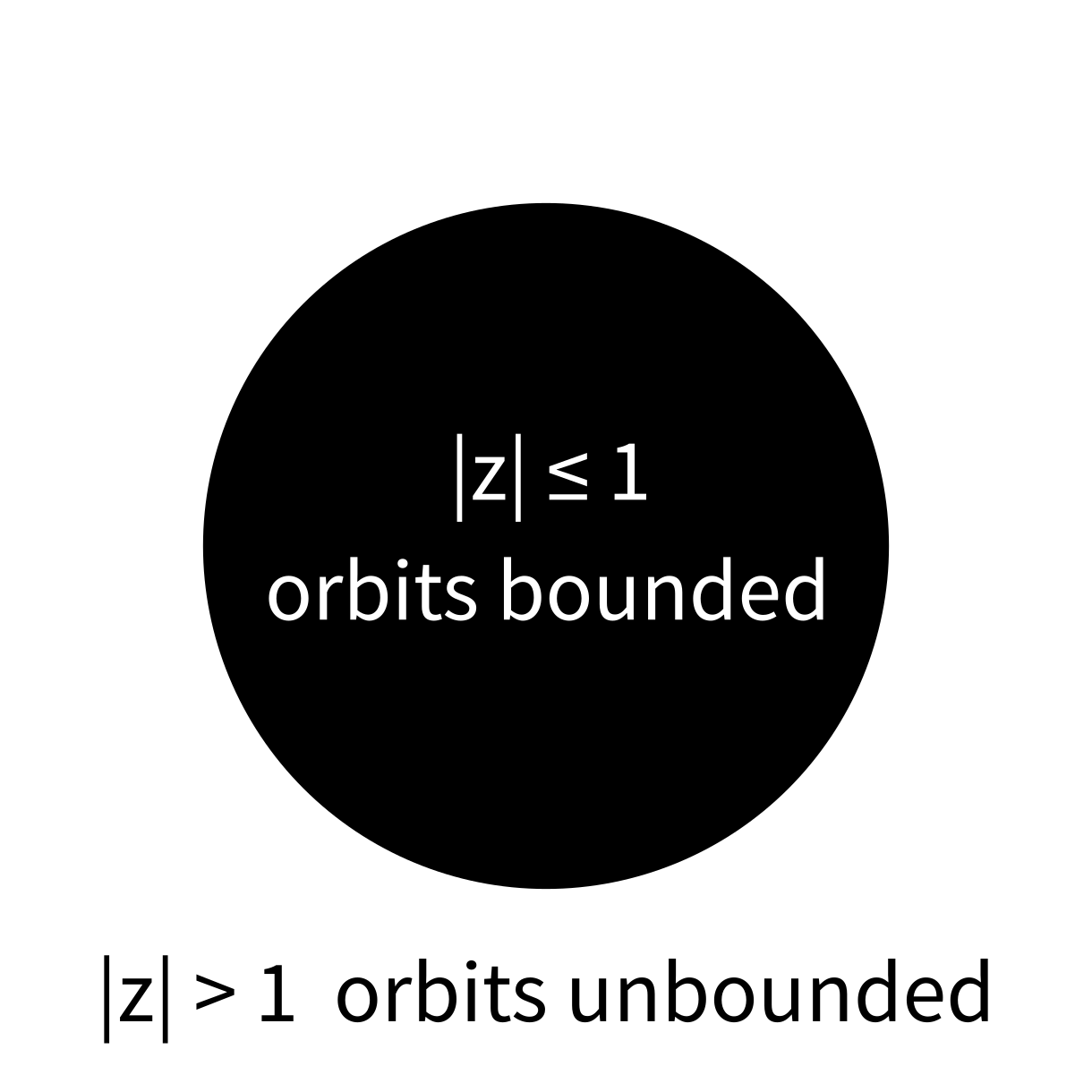
Filled Julia set

The filled Julia set of a polynomial $f(x)$, denoted $K_f$, is the set of complex numbers that have bounded orbits under $f$.

Named for mathematician Gaston Julia (1893-1978) who studied these sets starting in the 1920s.

$f(x)=x^2$

Next, let's look at $f(x) = x^2 - 1$.

First design

• Write a function to test orbit behavior of a point.
• Make a grid of points in $\mathbb{C}$ and test each one.
• Record the results in an image file (black=bounded, white=unbounded).

Divergence criterion

For $f(x) = x^2-1$, if $|a|\geq 2$, then $f^n(a) \to \infty$ as $n \to \infty$.

Improved design

• Make a grid of points in $\mathbb{C}$ and test each one.
• Use numpy array operations to apply $f$ to all of them at once, repeatedly.
• Optional: Keep track of ones that are already big, and don't apply $f$ to them.
• Record the results in an image file (black=bounded, white=unbounded).