Lecture 21

BST and tree traversals

MCS 275 Spring 2021
Emily Dumas

Lecture 21: BST and tree traversals

Course bulletins:

• Worksheet 8 available.
• Thursday discussion students: Please attempt problem 1 before discussion.

Sample code

As a reminder, all the tree sample code is available.

Insert

Take a Node object and add it to the tree in a place that maintains the BST property.

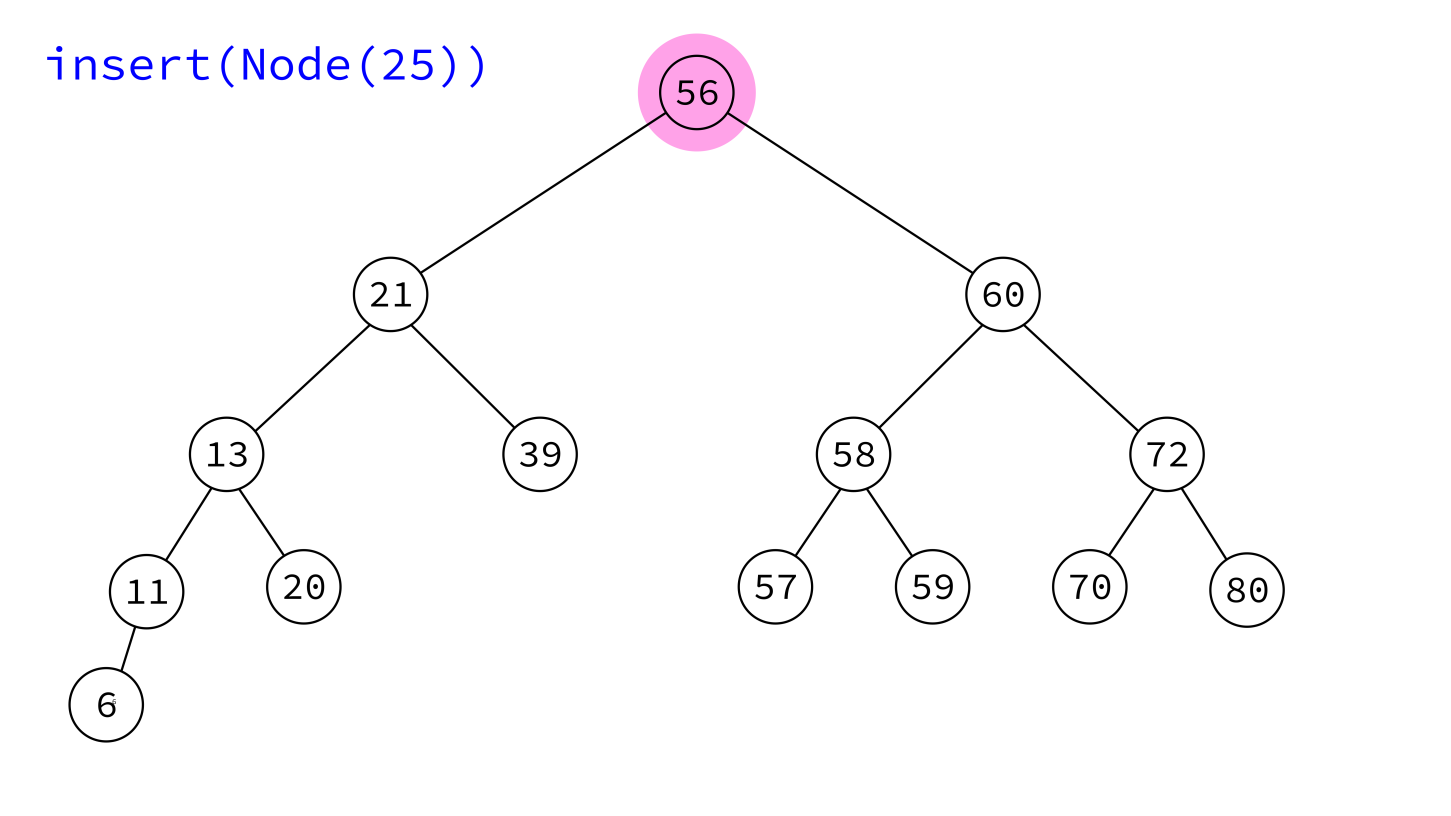
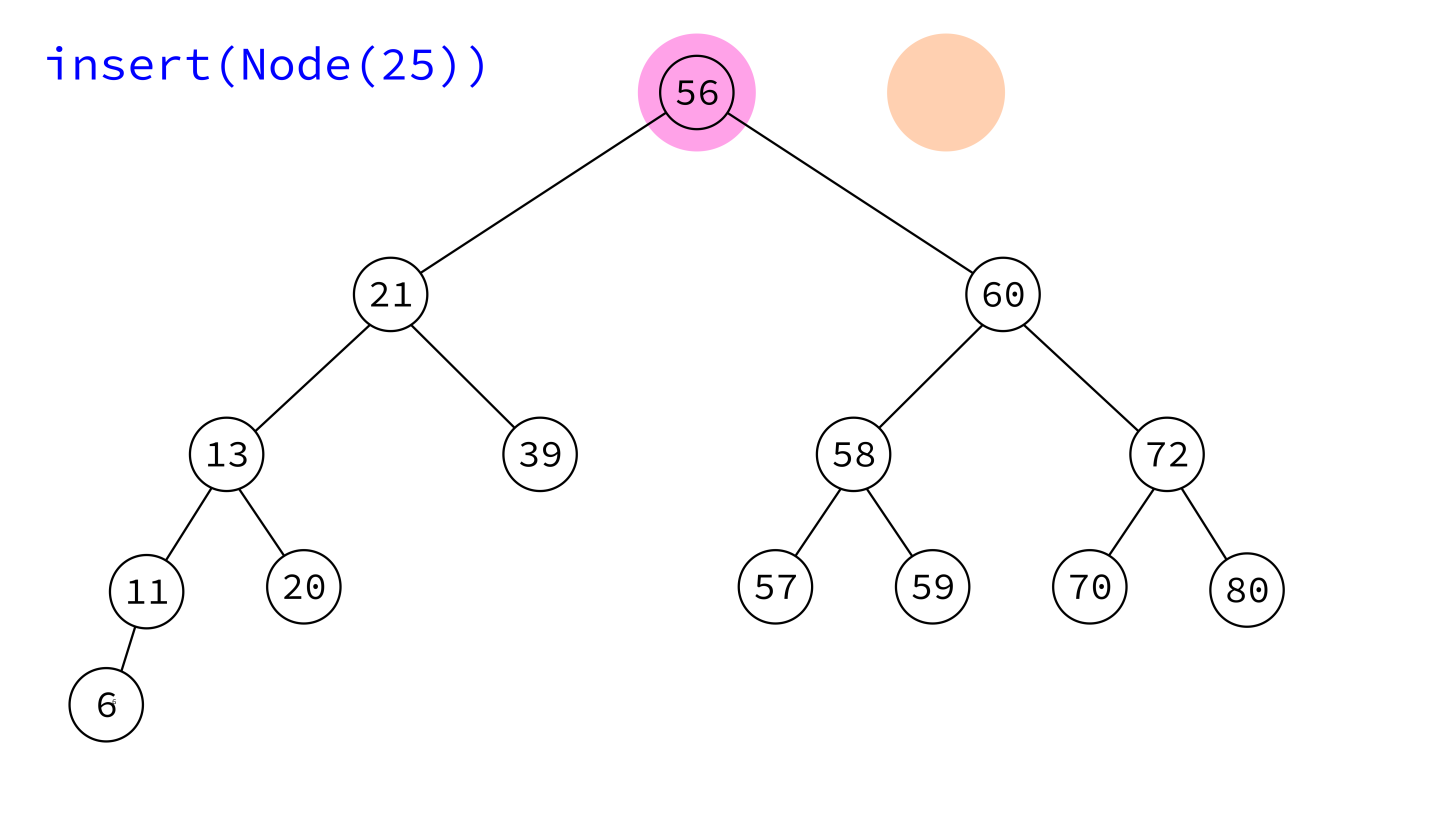
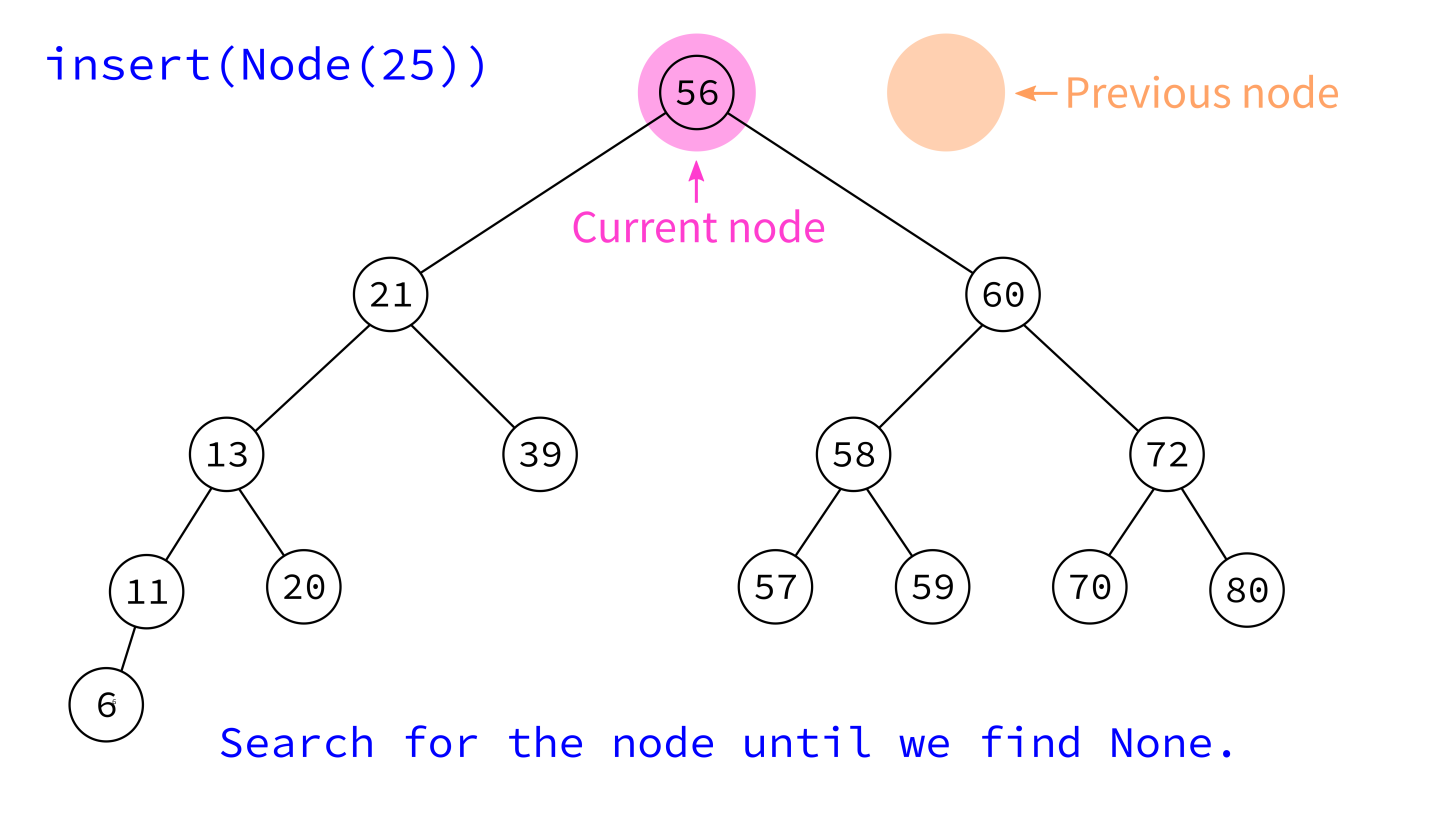
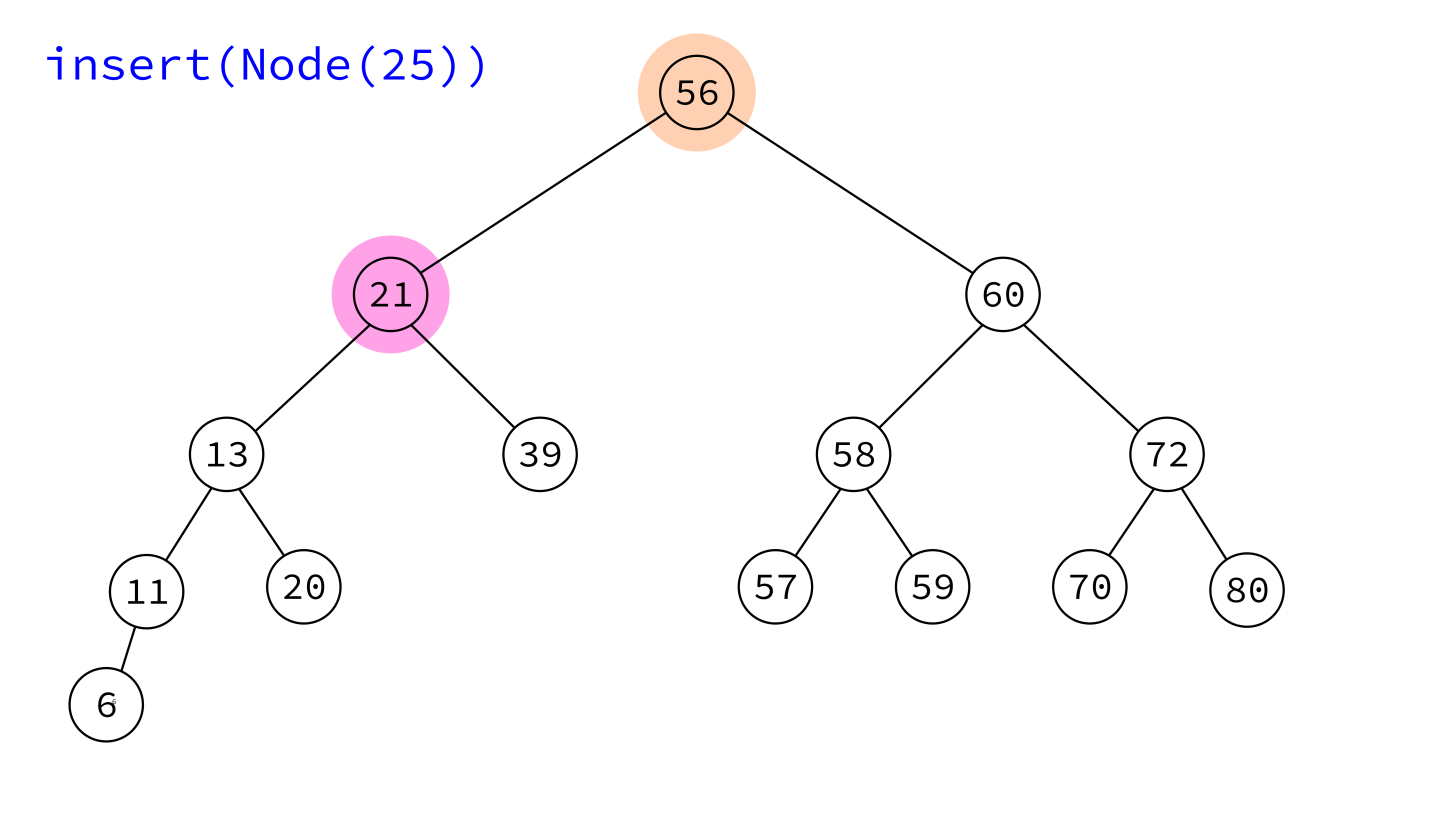
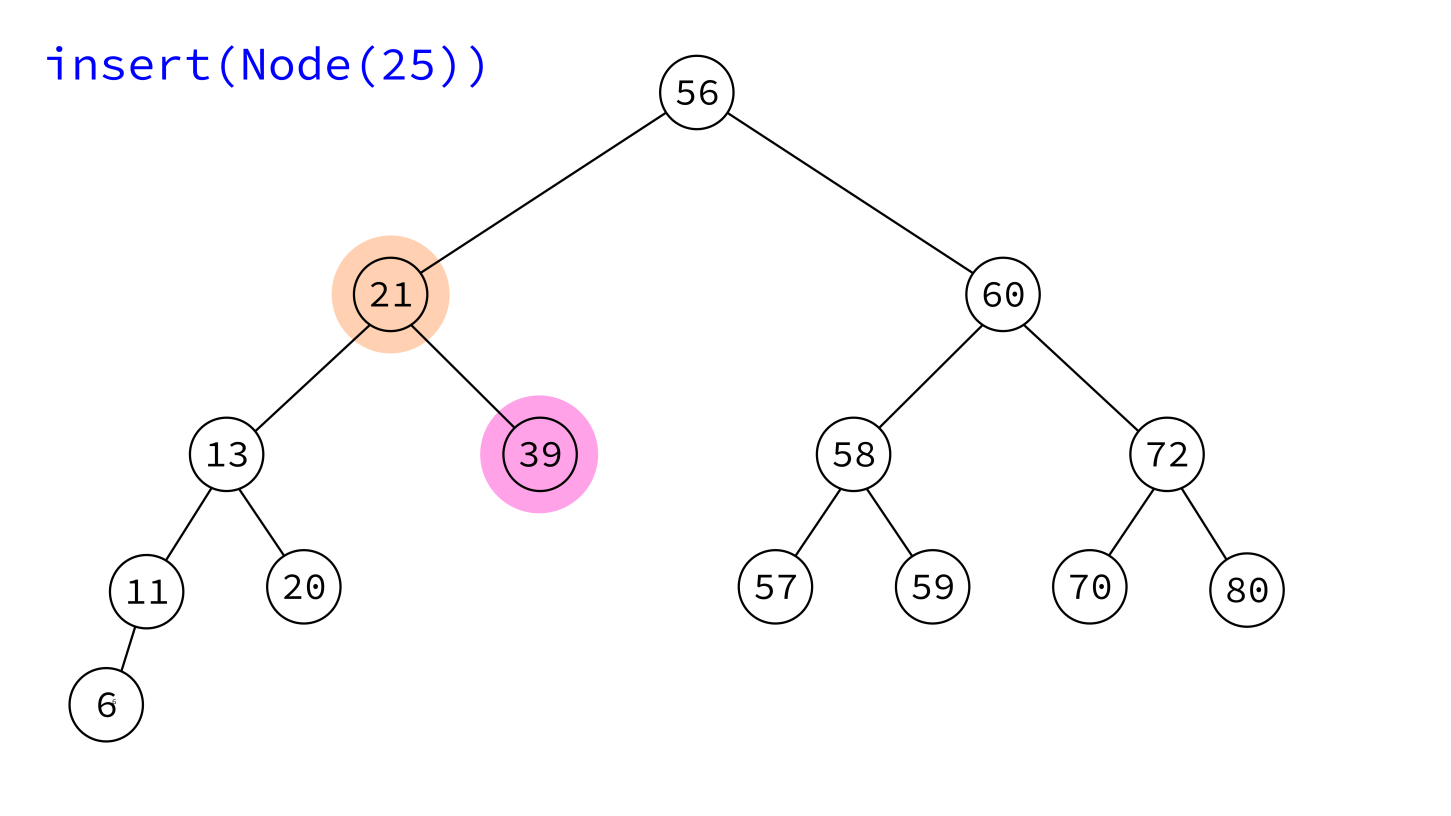
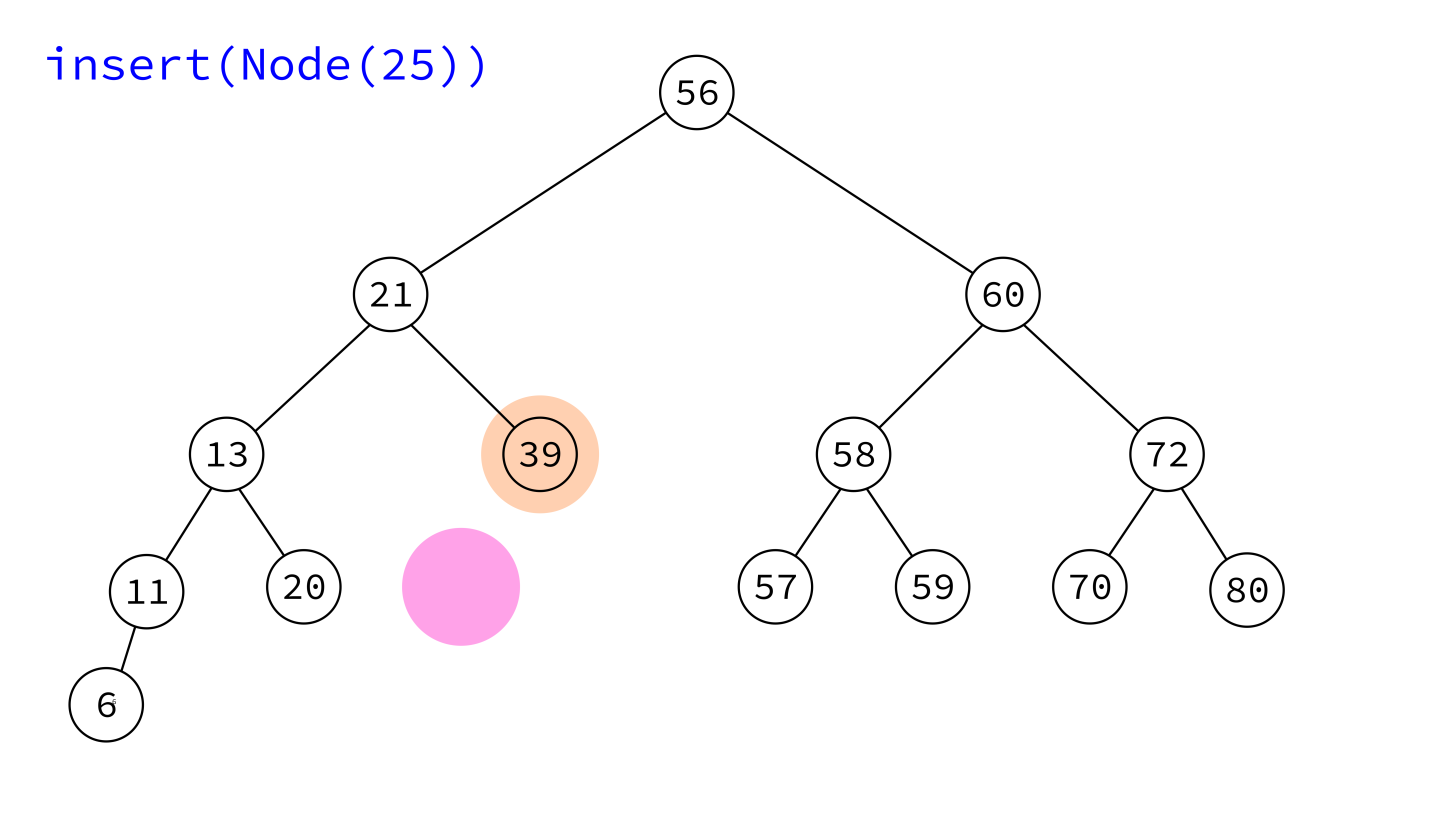
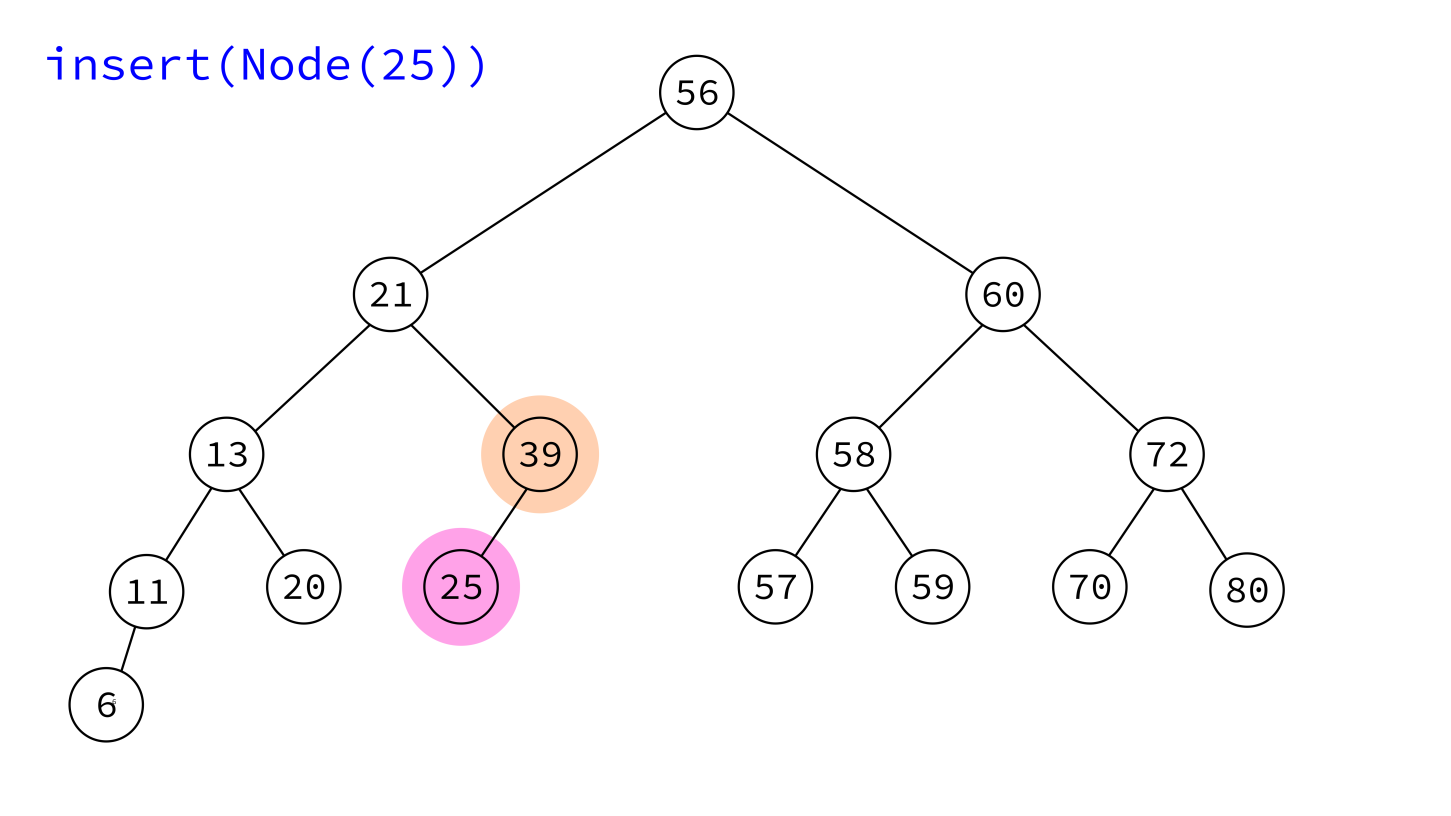
The node must have its key set, but not its parent and children. Insert will handle those.

IntegerSet

As a sample application of BST, we can make a class that stores a set of integers, supporting membership testing and adding new elements.

Compare alternatives:

• Unsorted list - fast to insert, but slow membership test
• Sorted list - fast membership test, slow insert

Implementation Hiding

To use BST, you need to know about and work with Node objects.

In contrast, IntegerSet has an interface based directly on the values to be stored. It hides the fact that its implementation uses a BST.

Walking a tree

Back to discussing binary trees (not necessarily BST).

For some purposes we need to visit every node in a tree and perform some action on them.

To do this is to traverse or walk the tree.

Named traversals

The three most-often used recursive traversals:

• preorder - Node, left subtree, then right subtree.
• postorder - Left subtree, right subtree, then node.
• inorder - Left subtree, node, then right subtree.

Note: They all visit left child before right child.

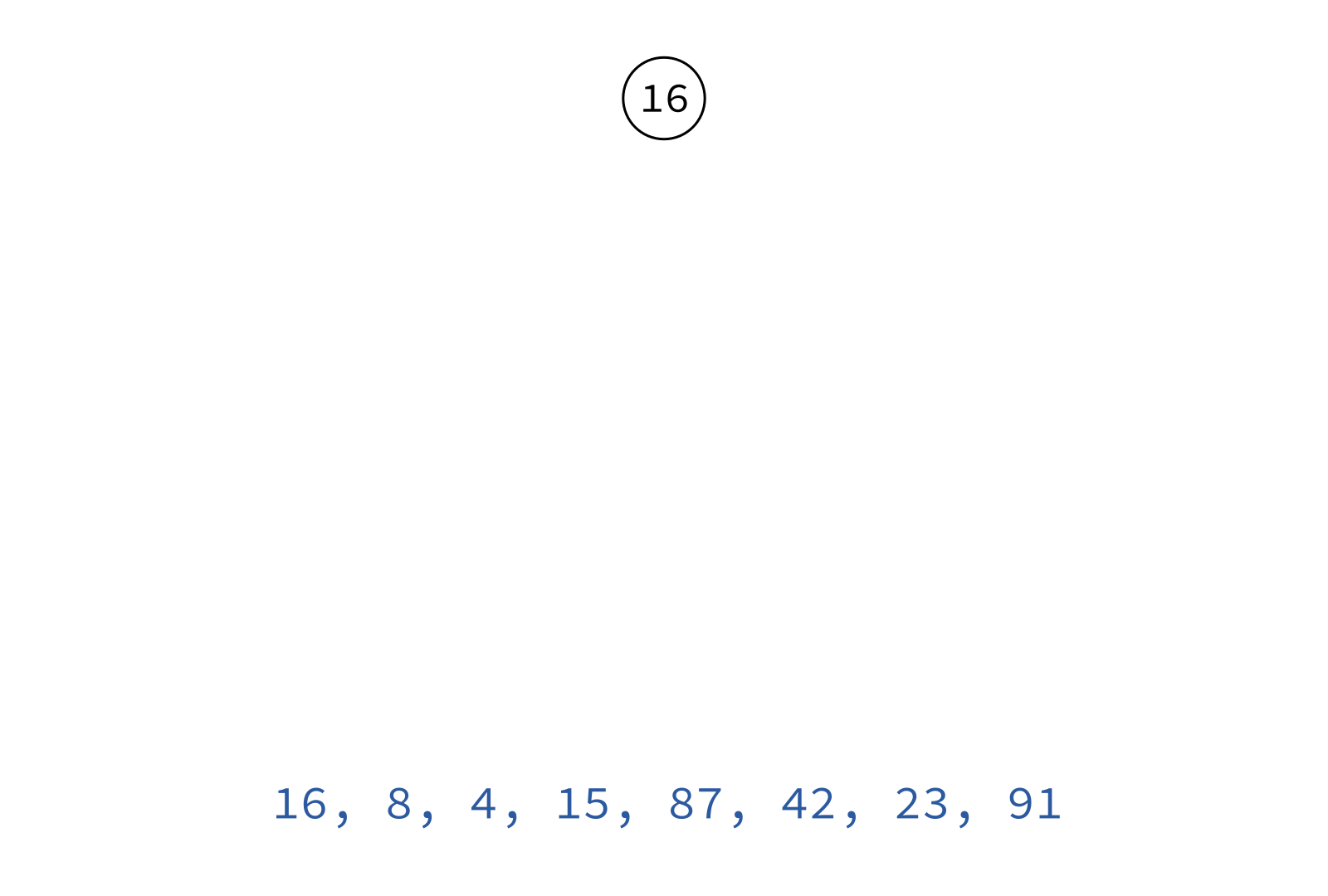
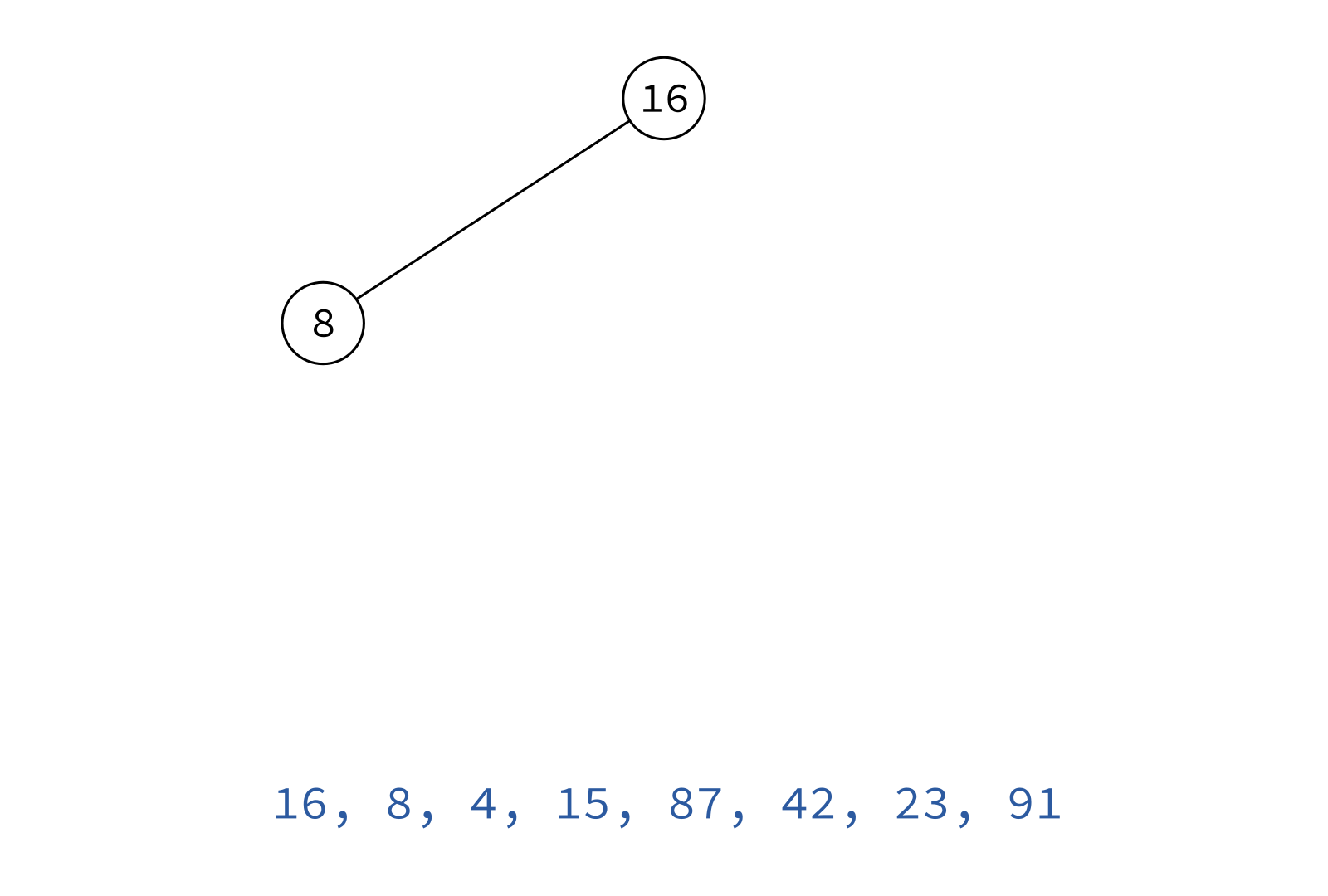
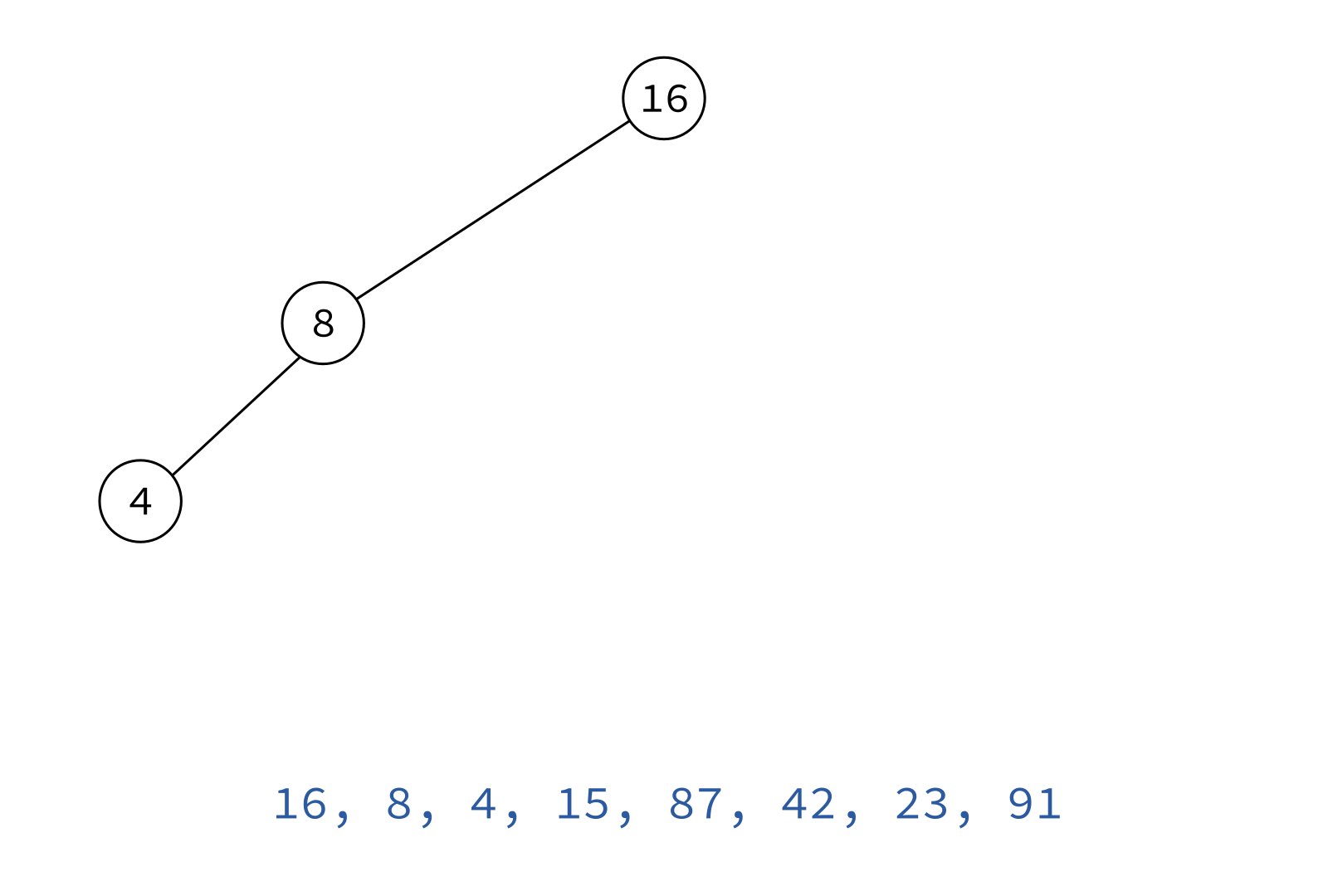
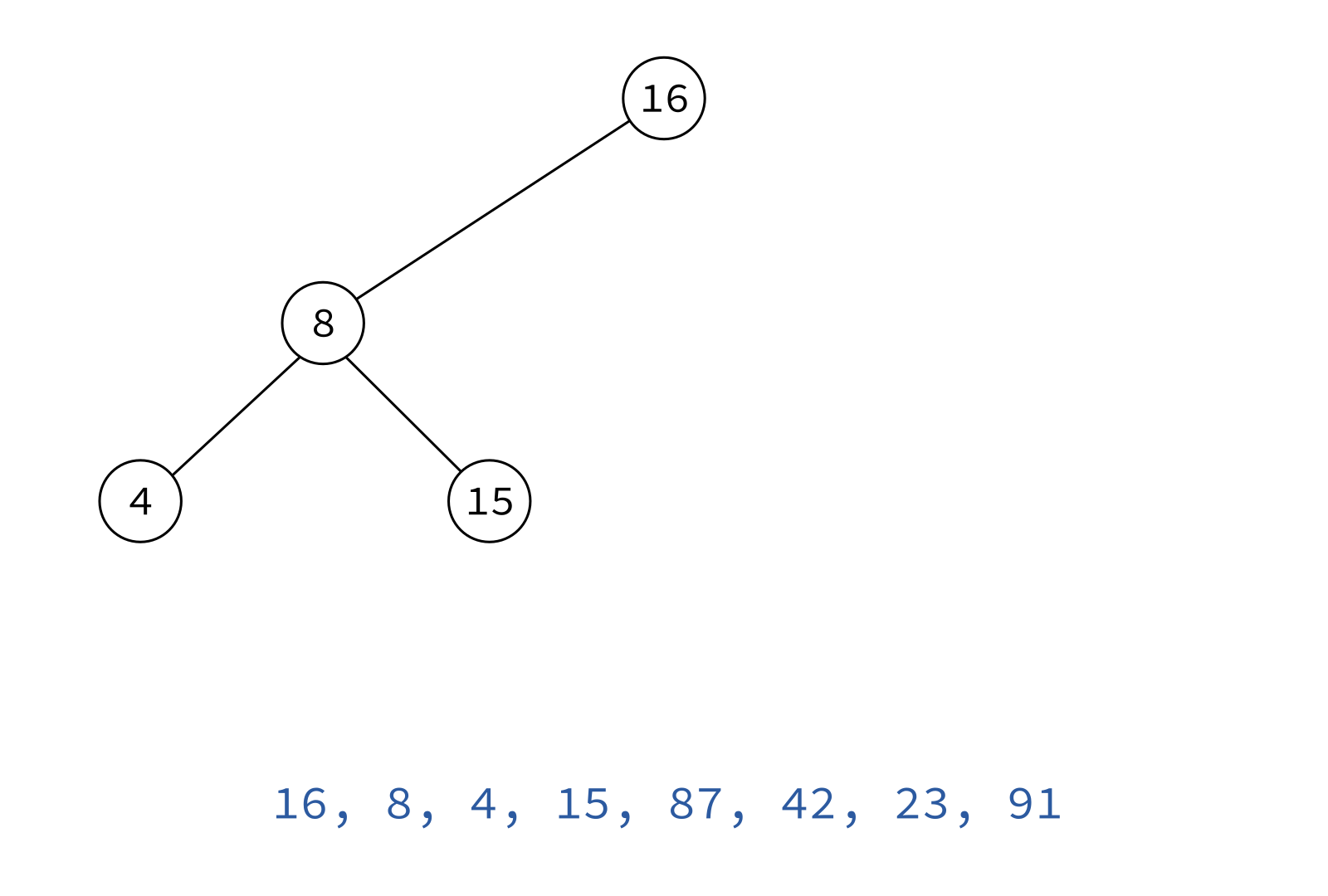
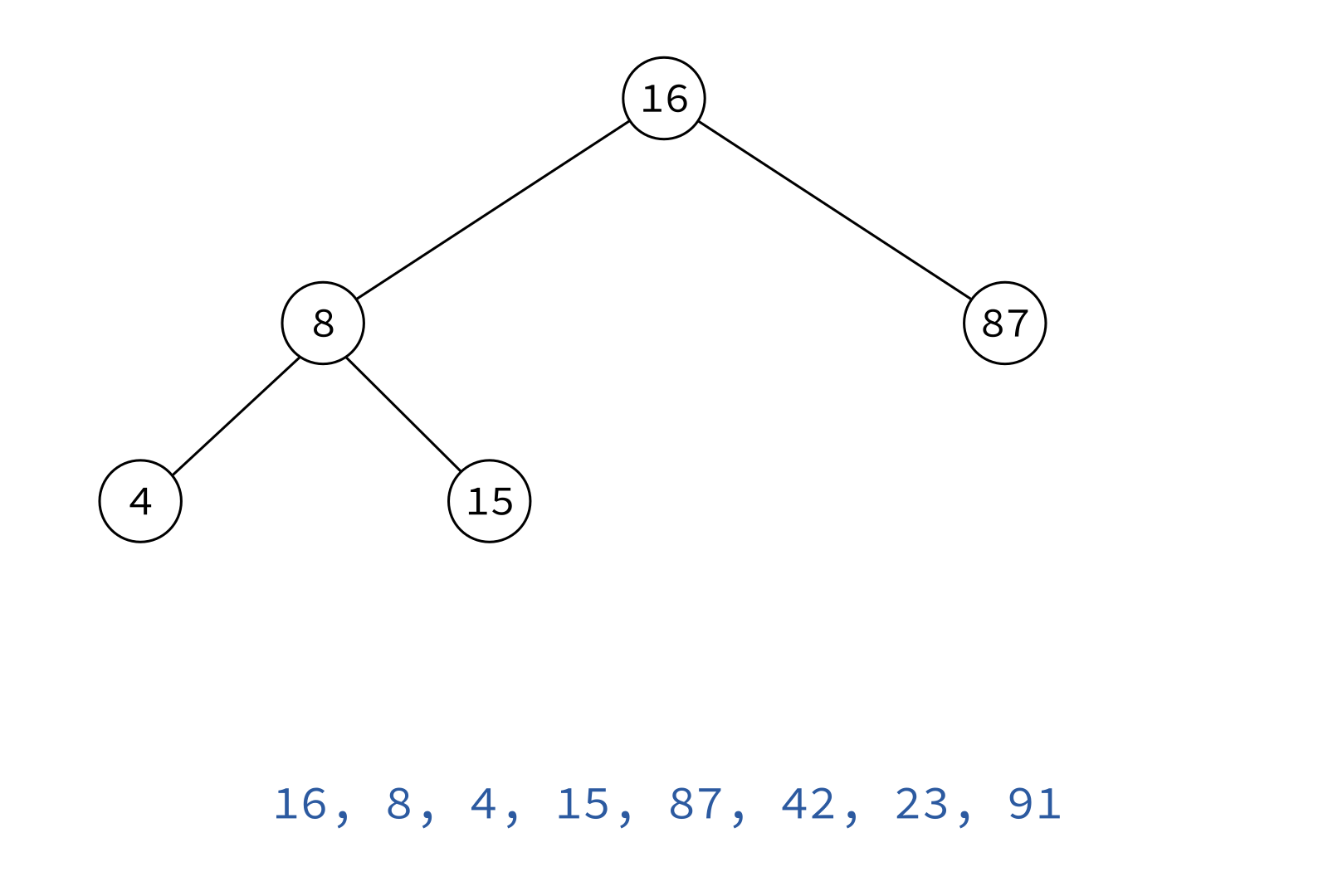
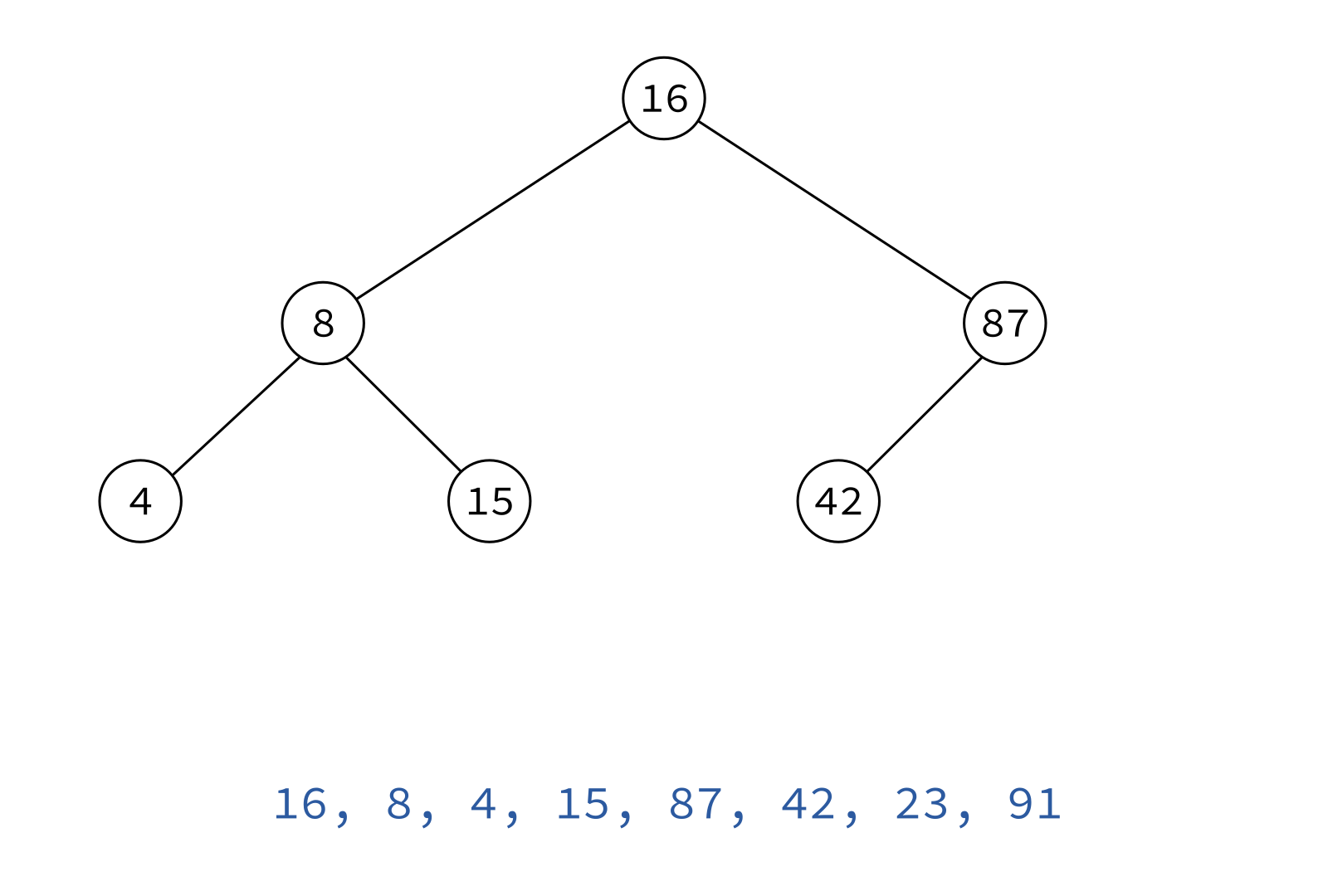
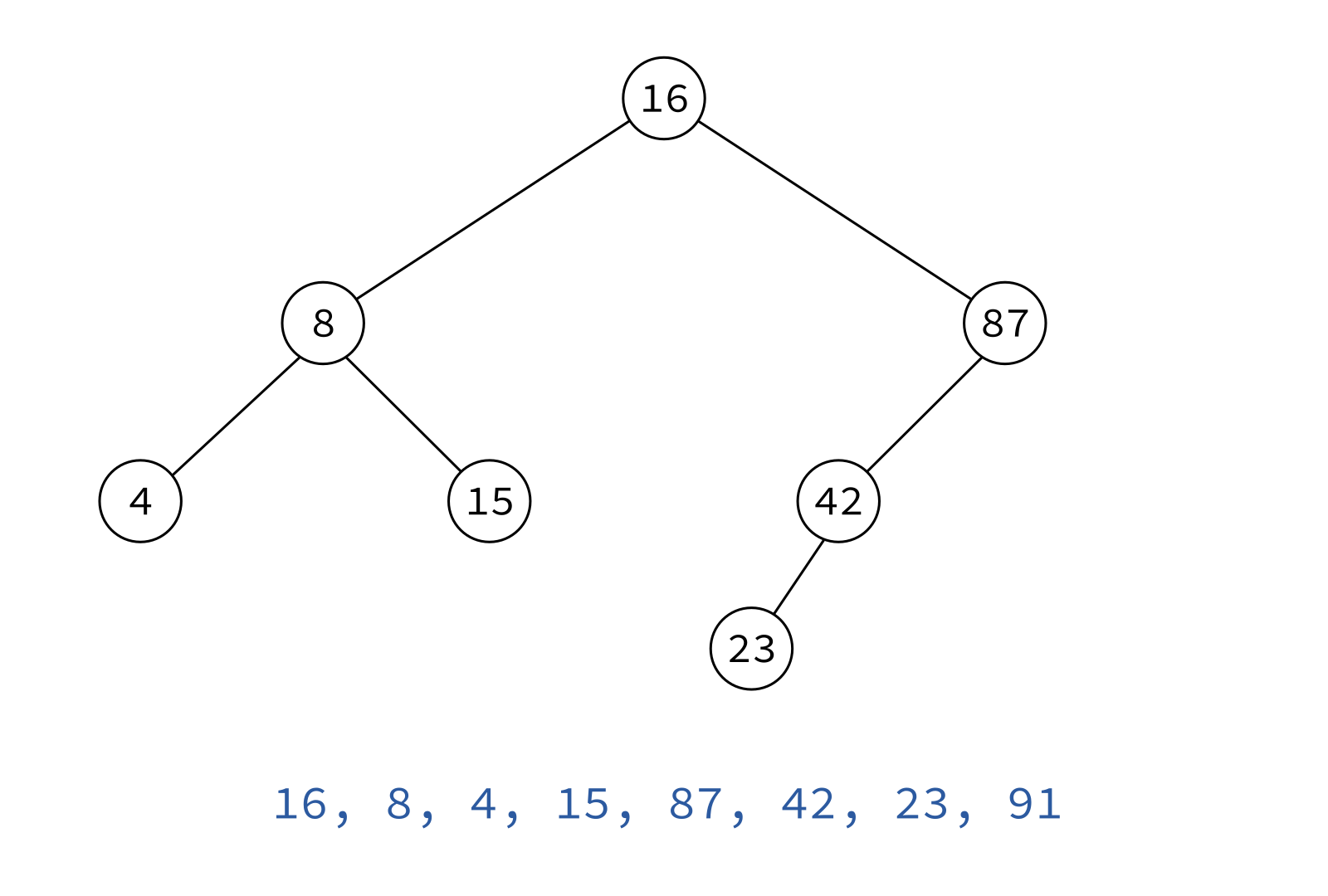
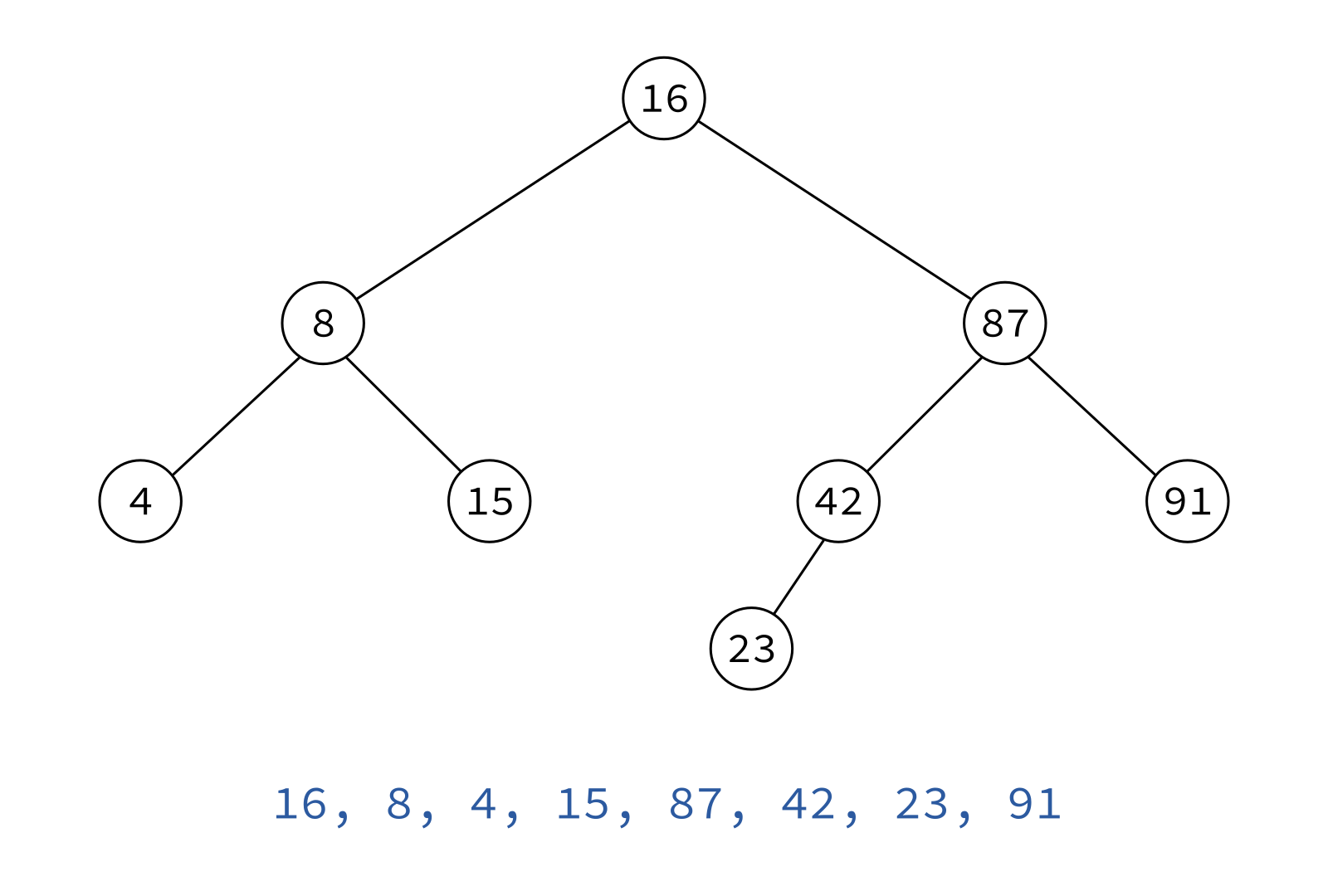
Preorder traversal

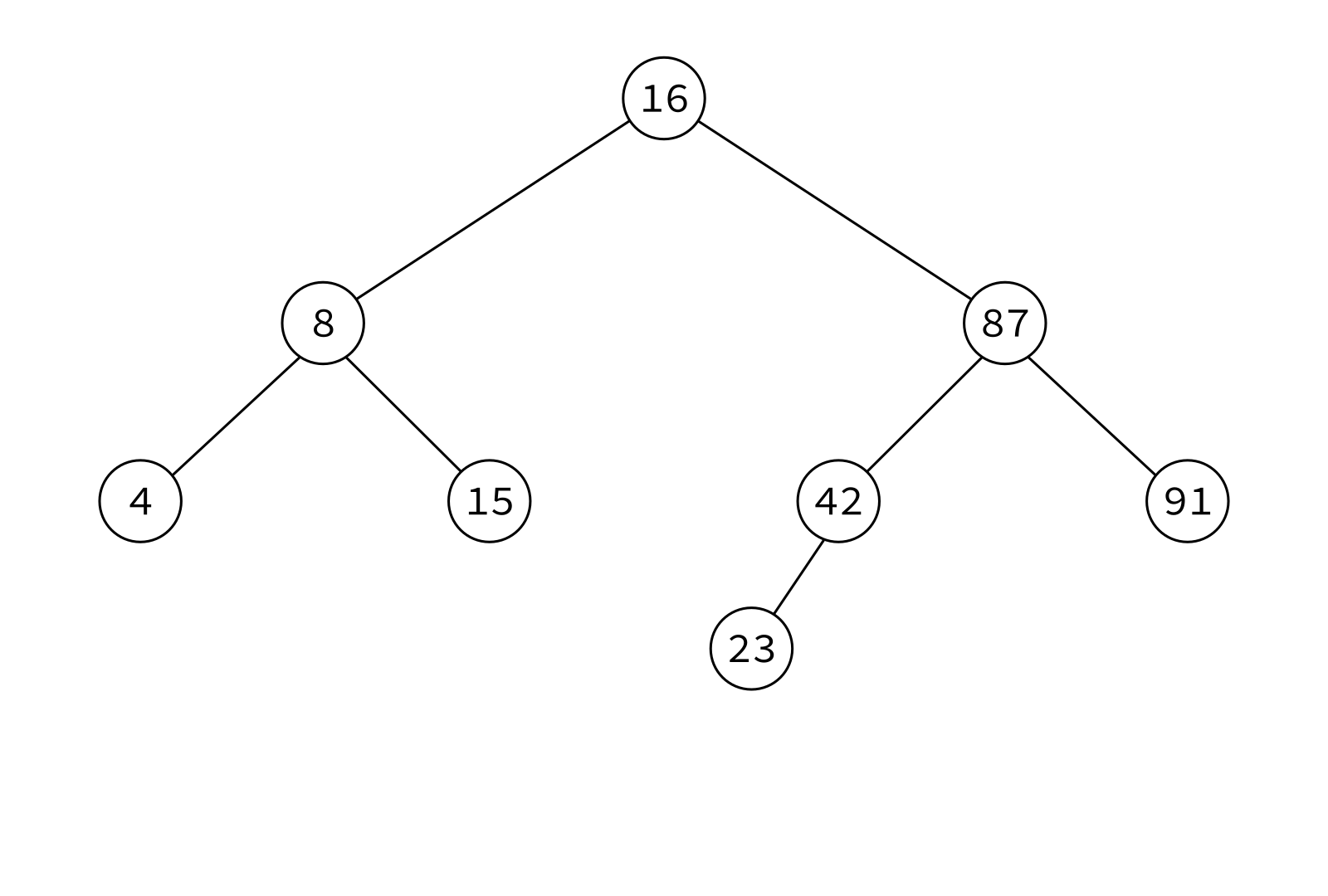
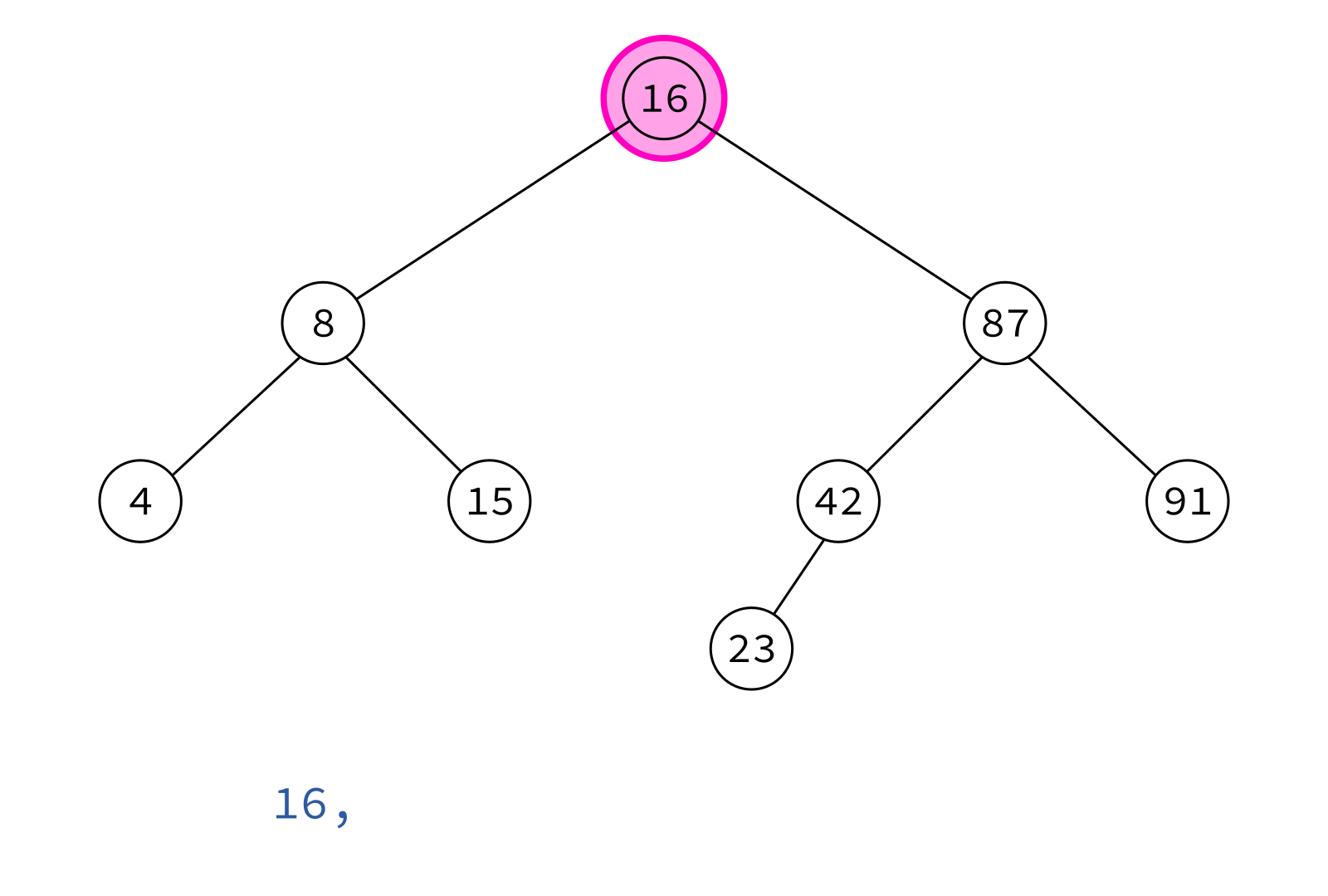
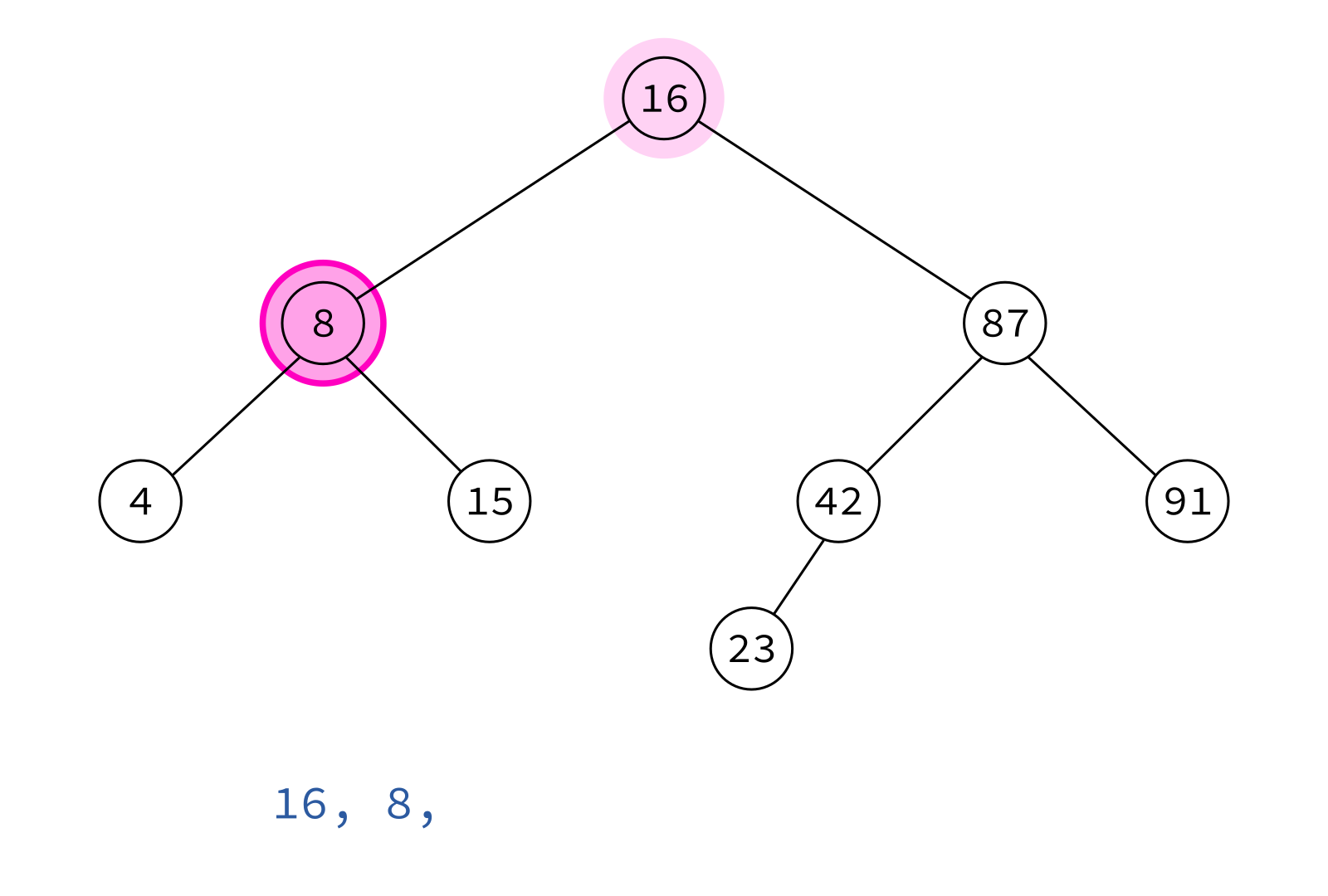
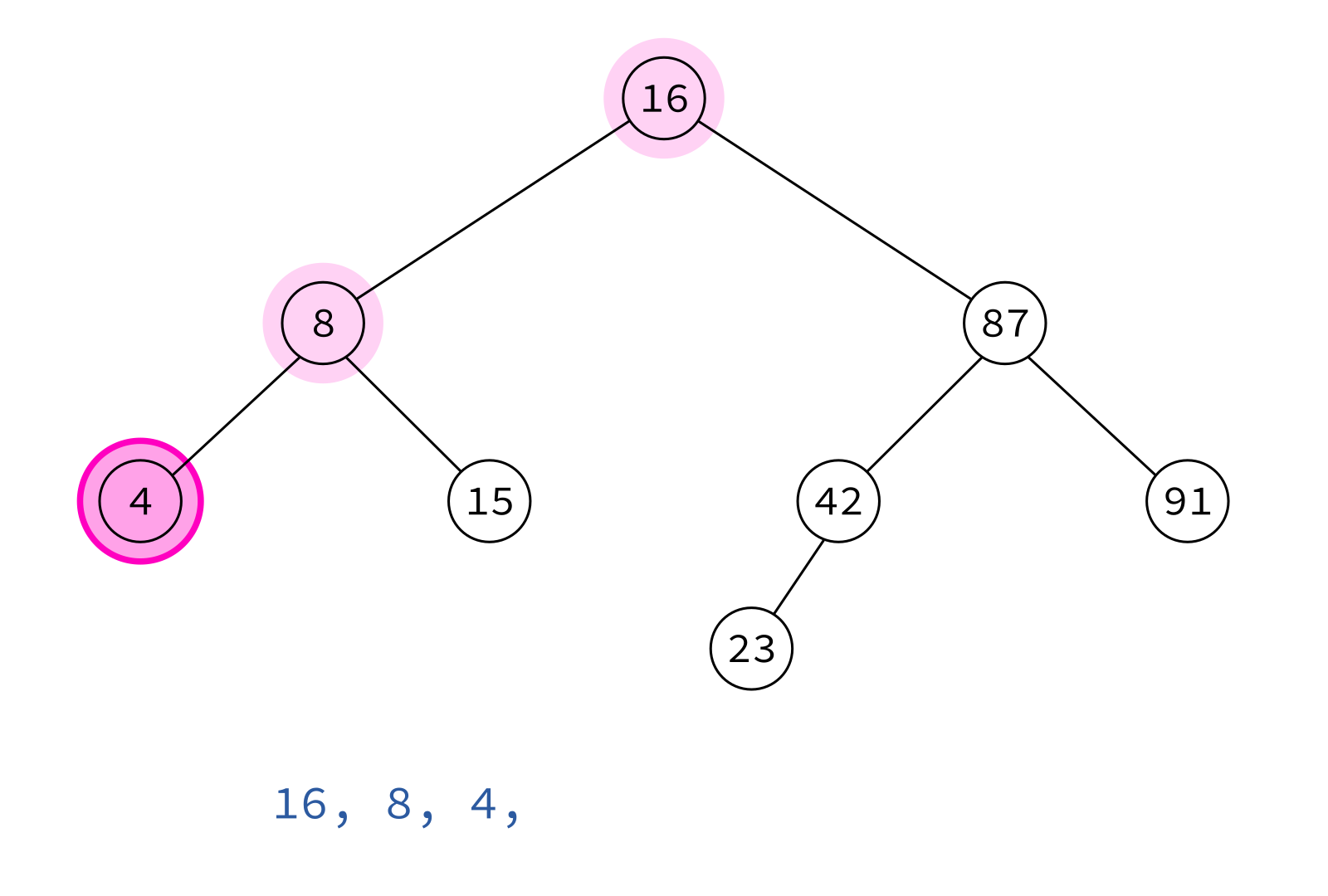
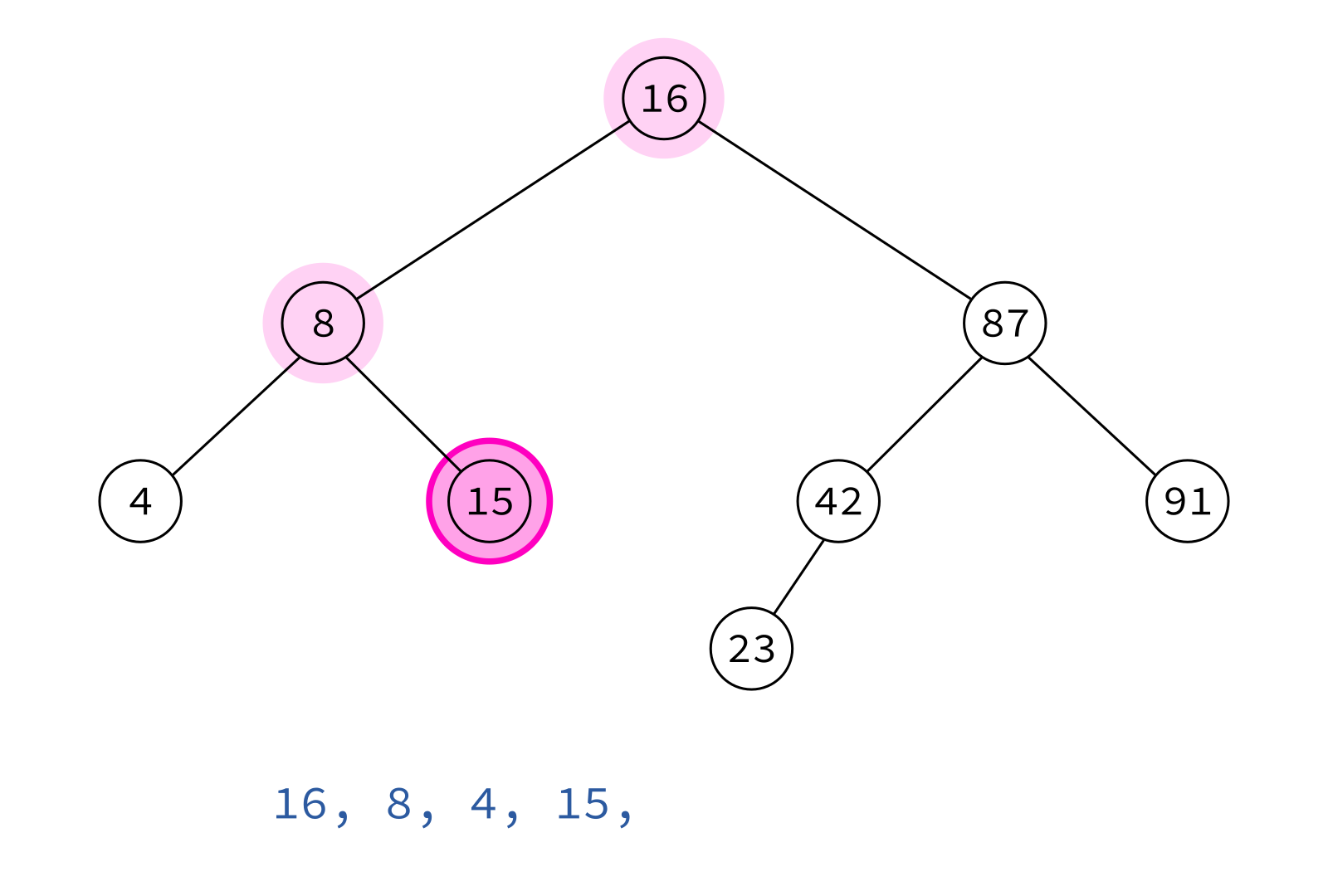
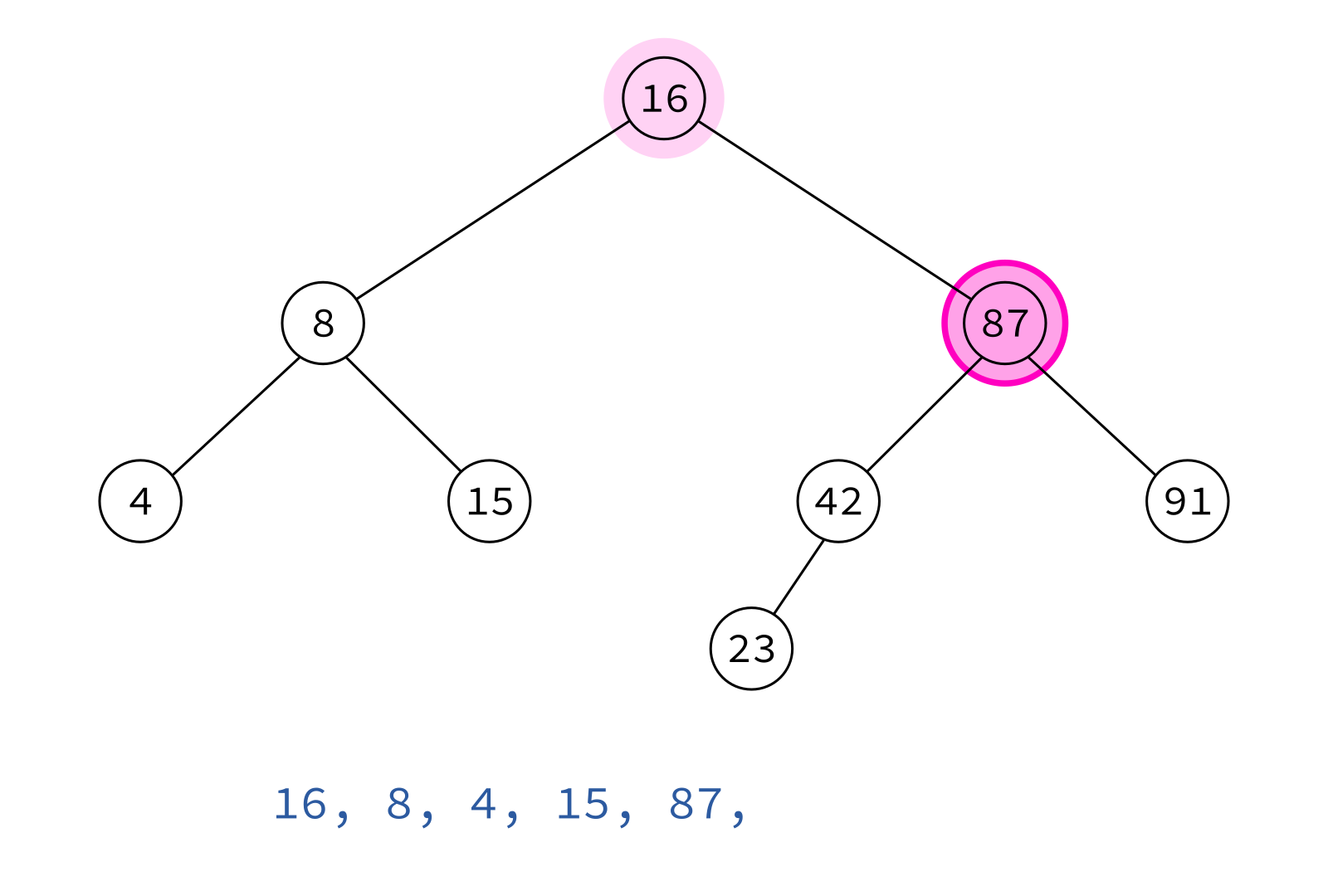
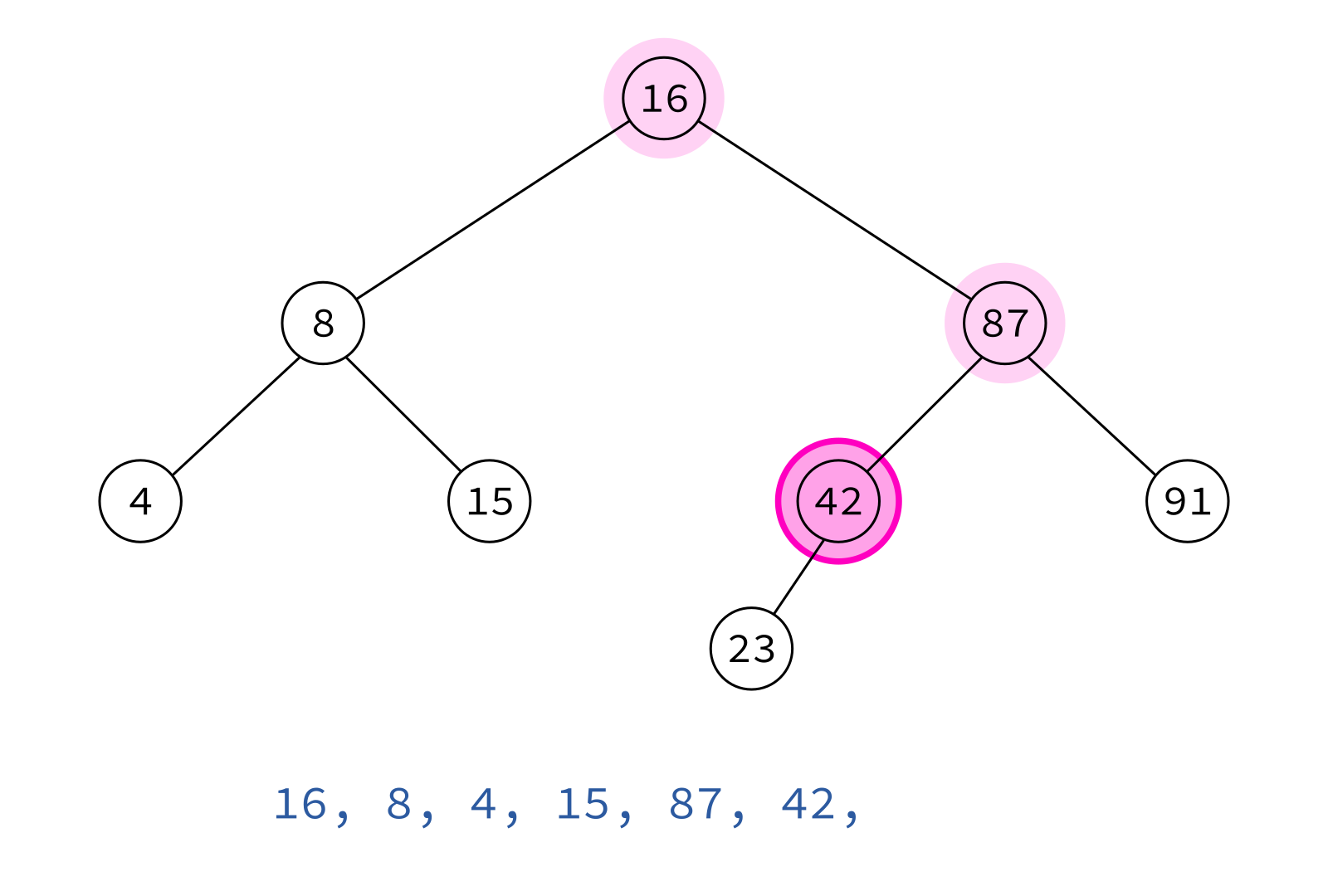
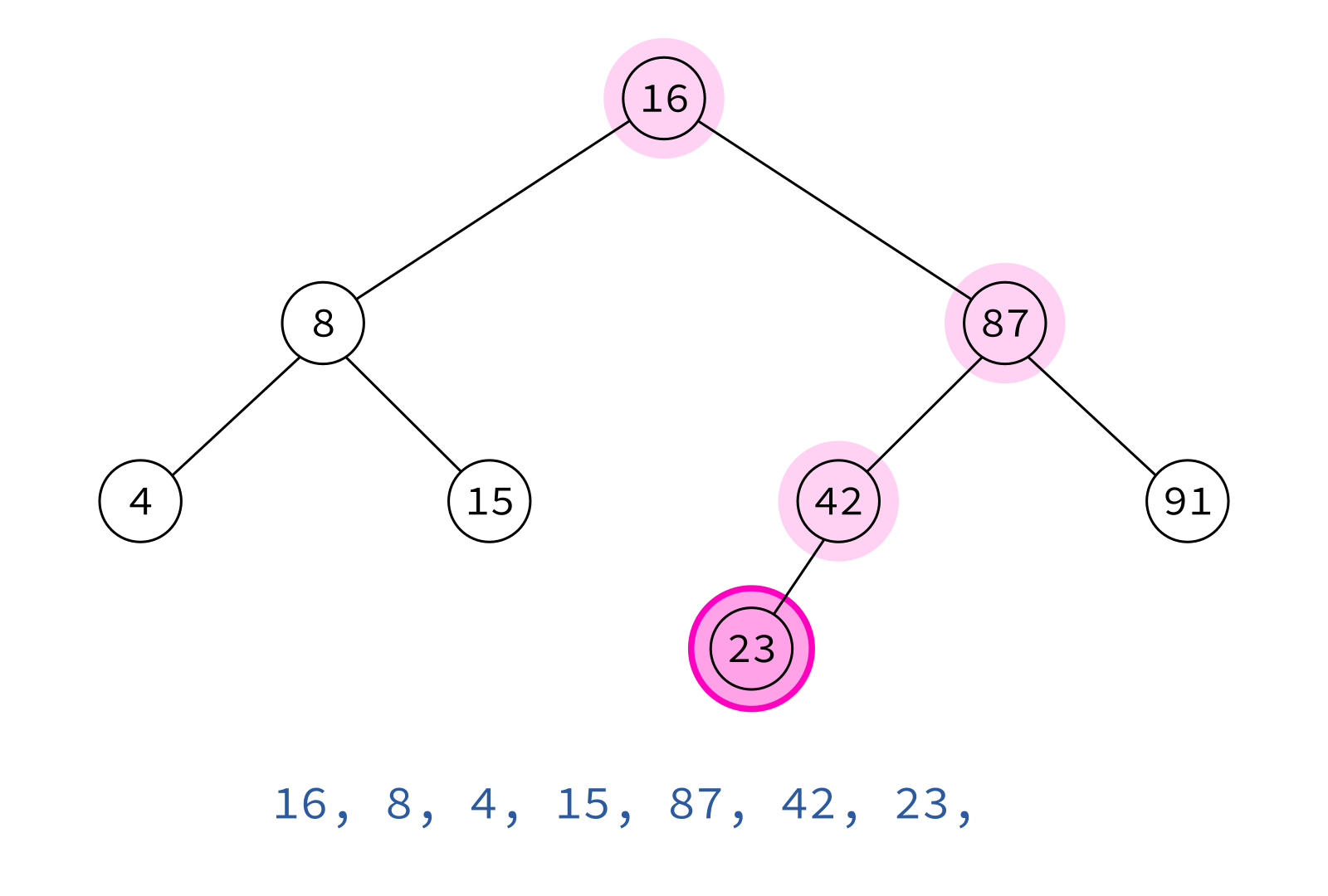
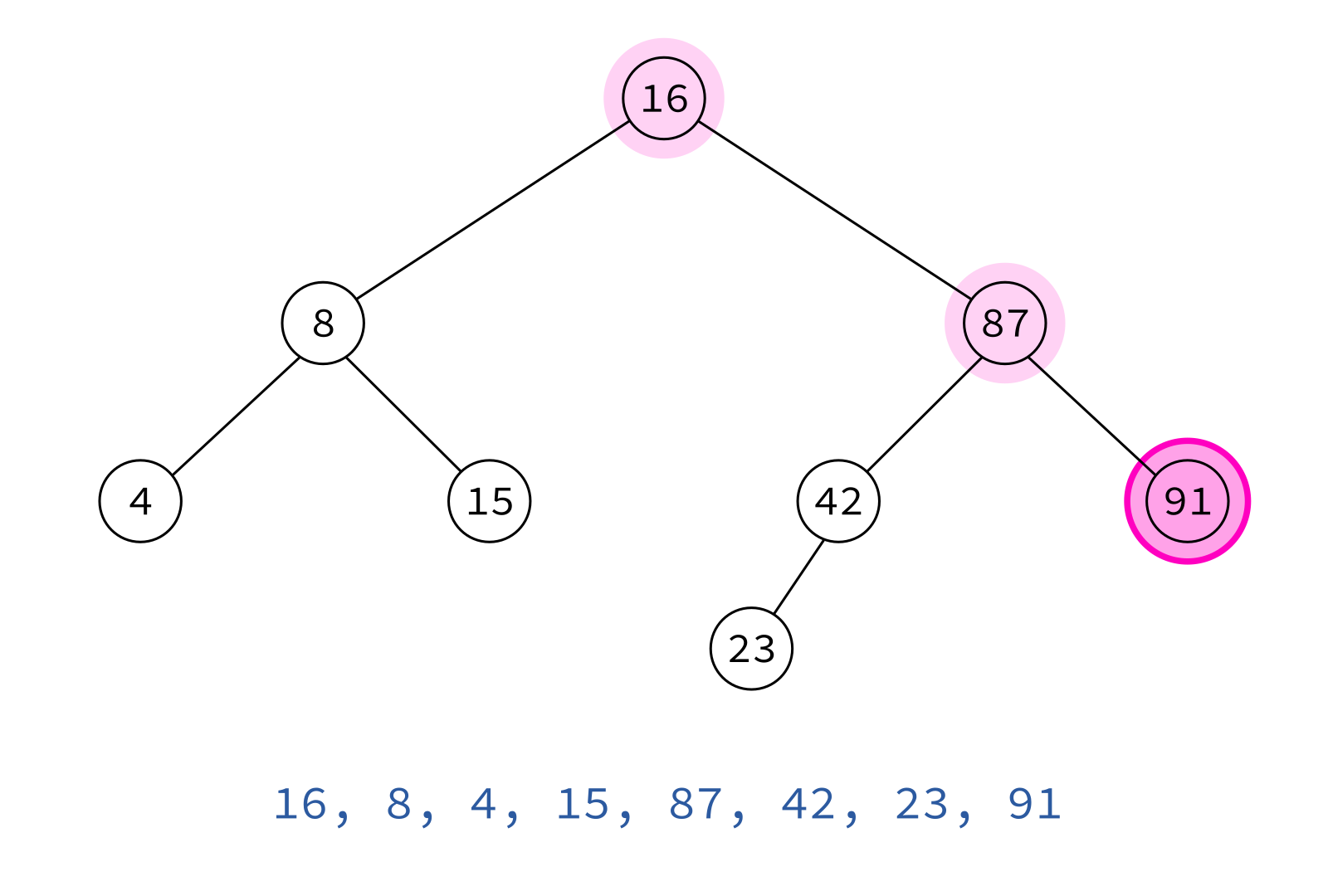
node, left, right

Preorder traversal

Typical use: Make a copy of the tree.

Insert the keys into an empty BST in this order to recreate the original tree.

Postorder traversal

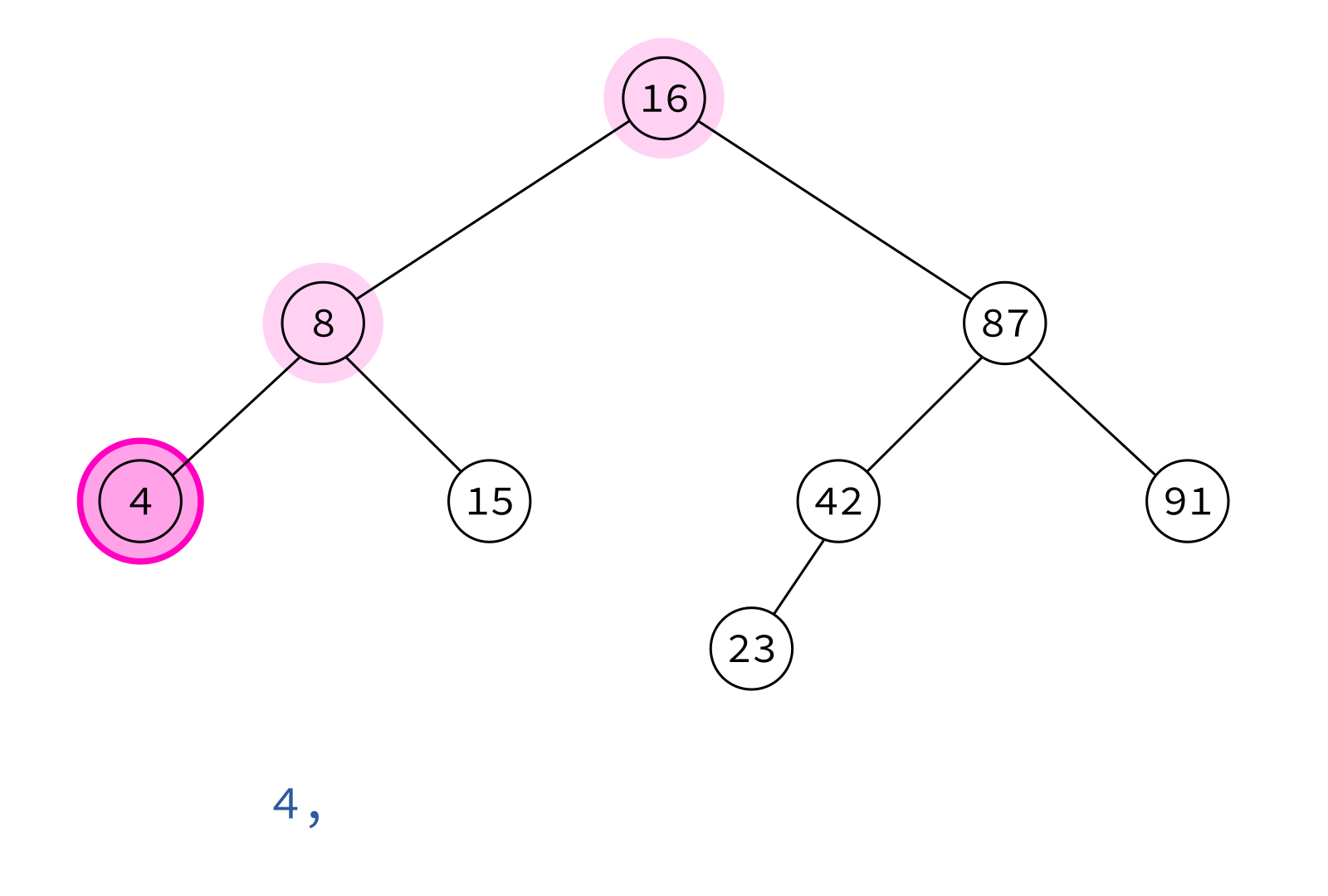
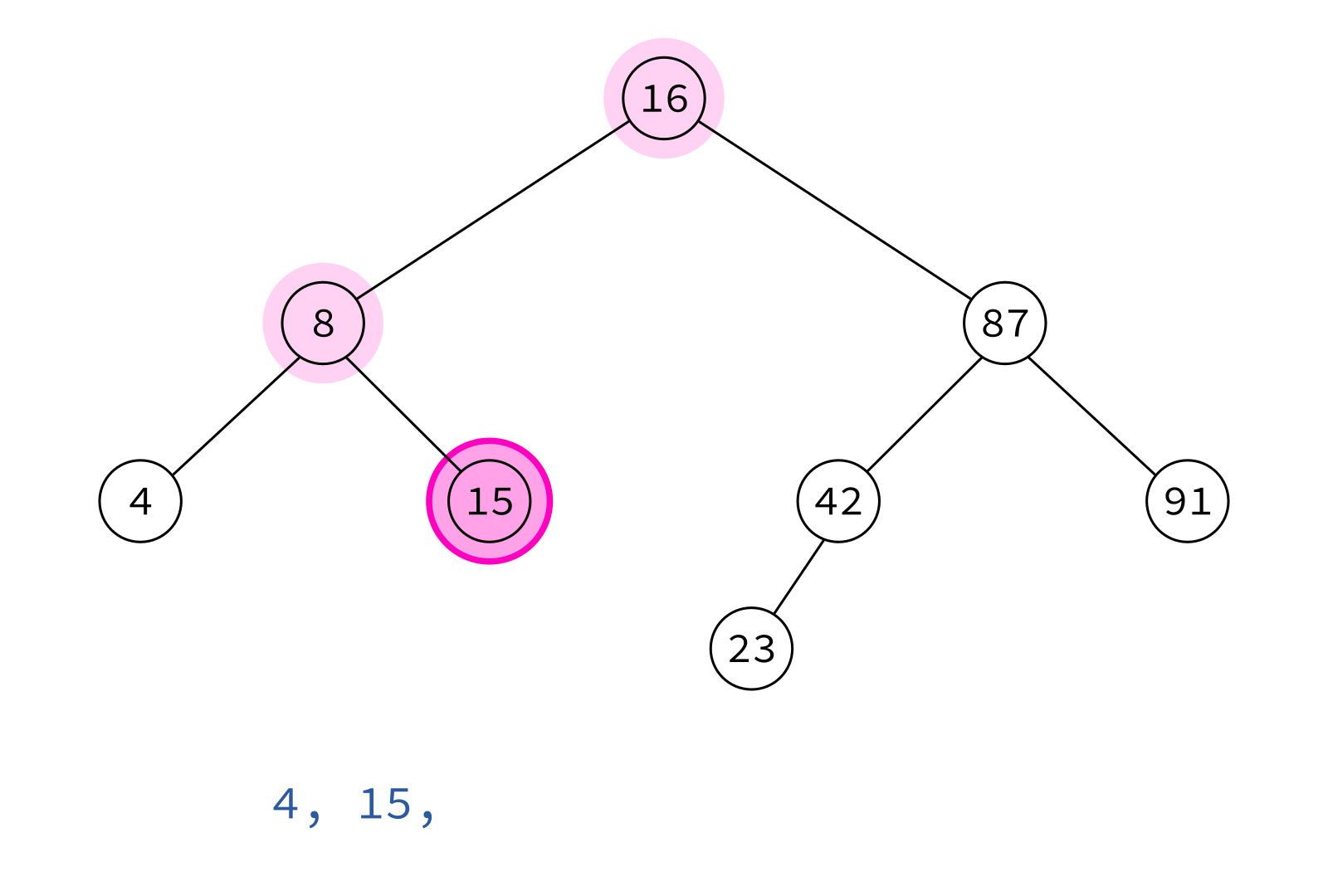
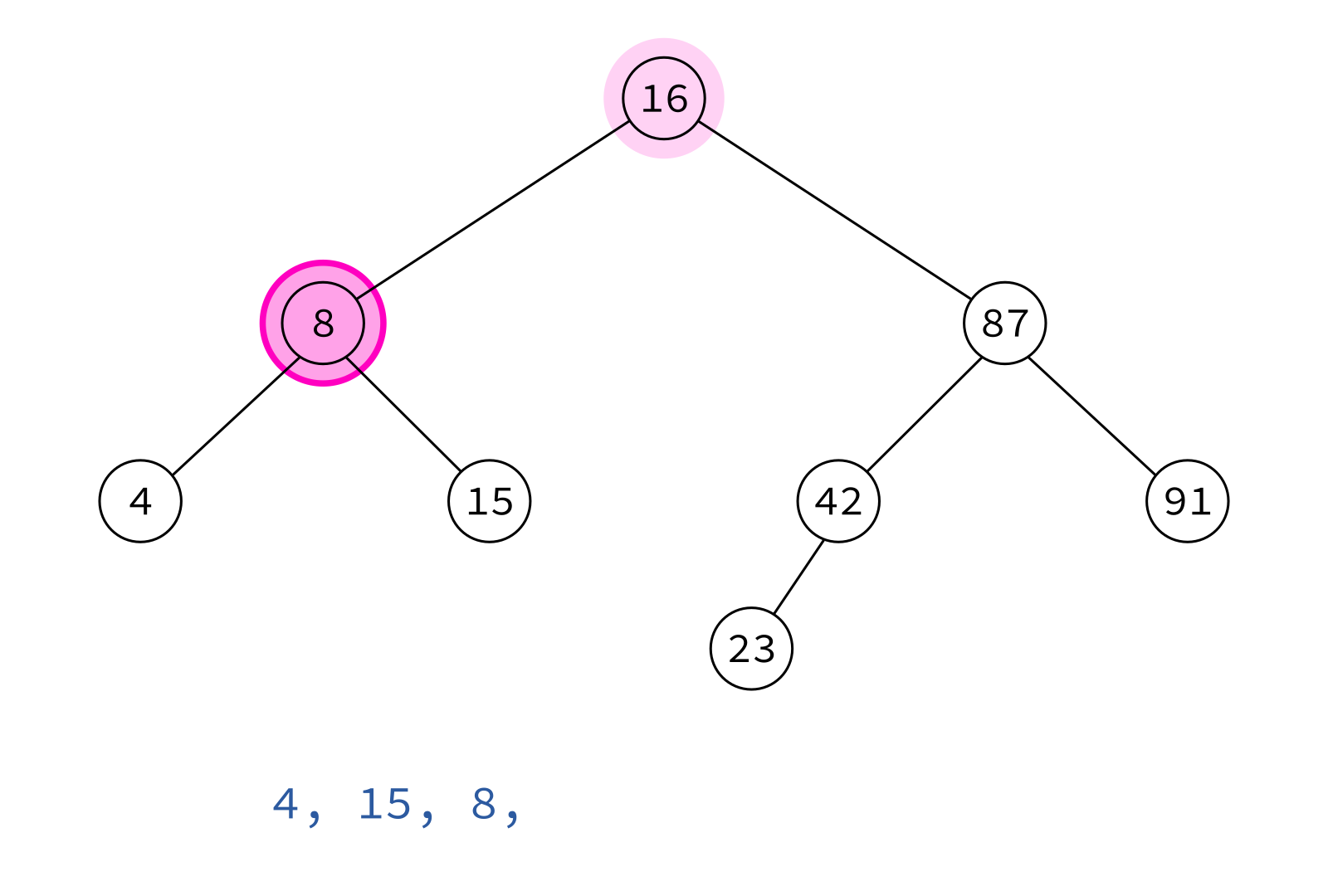
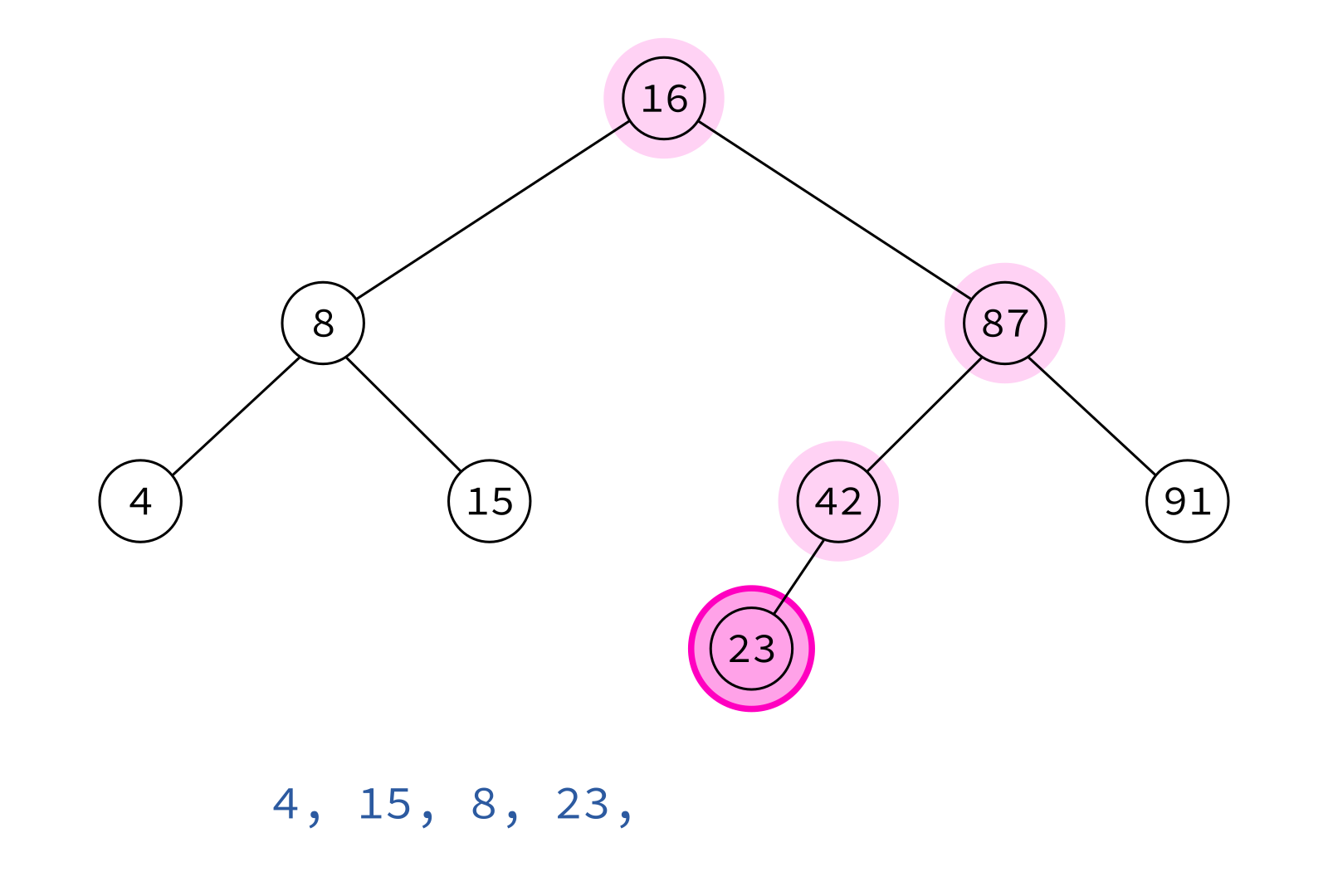
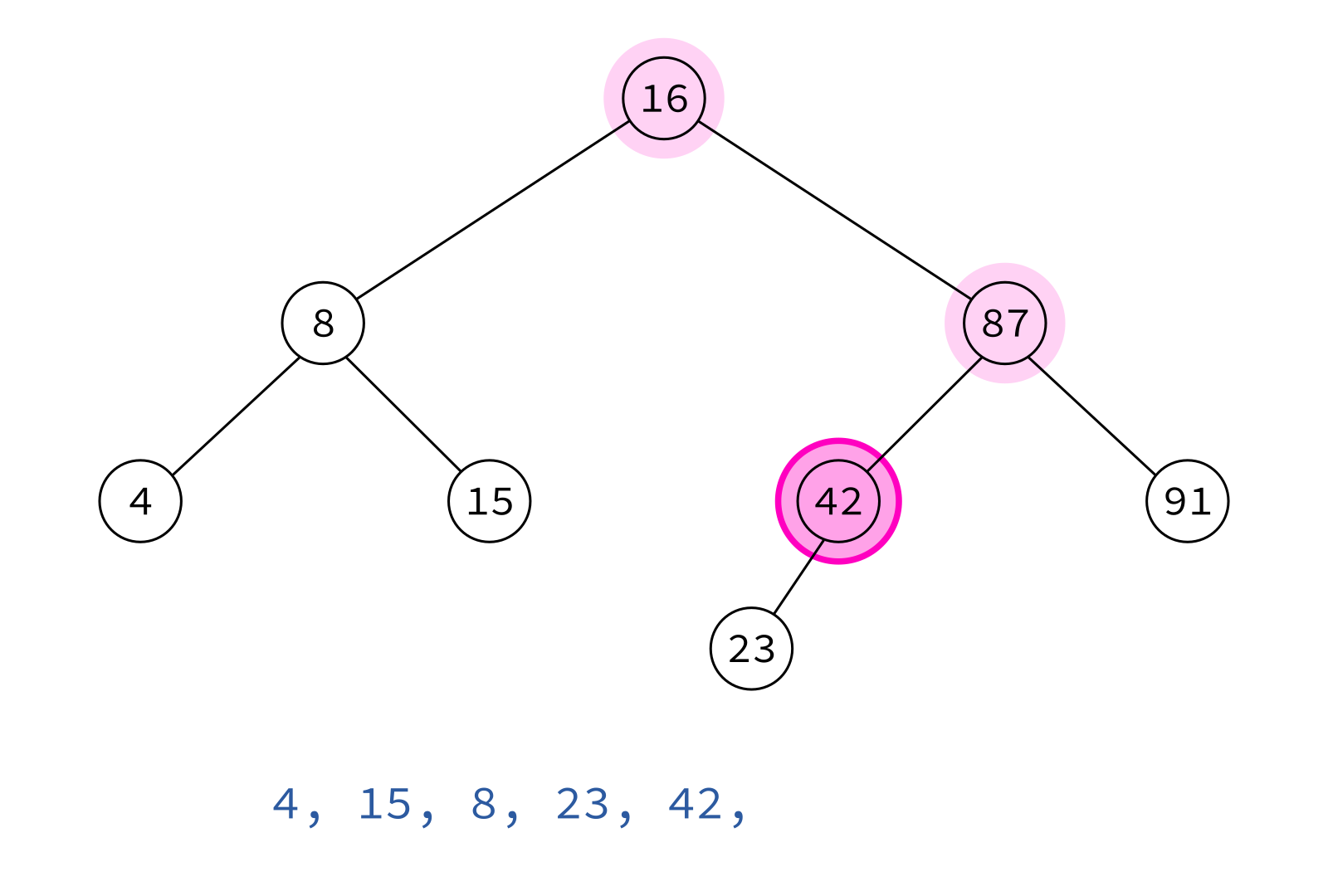
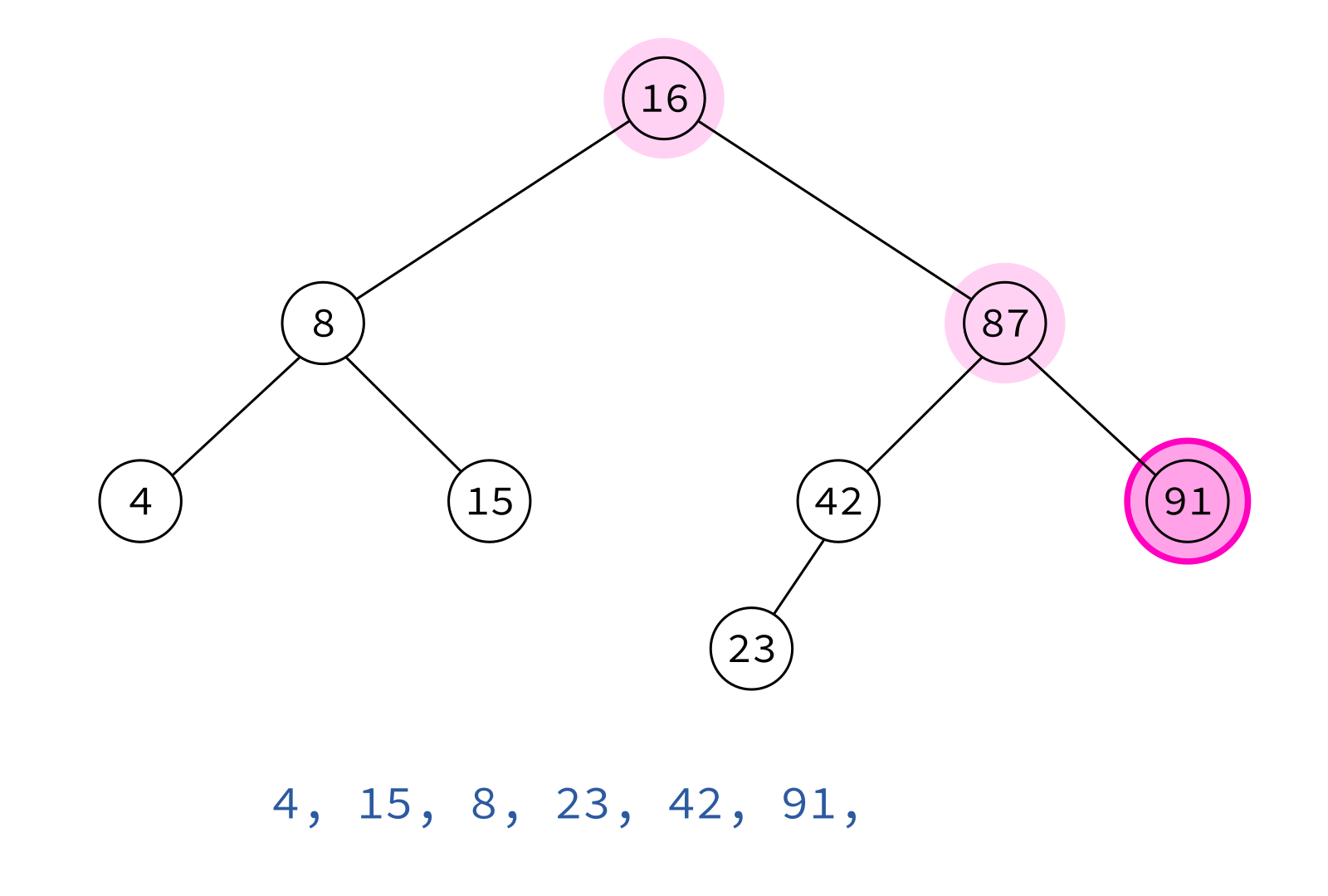
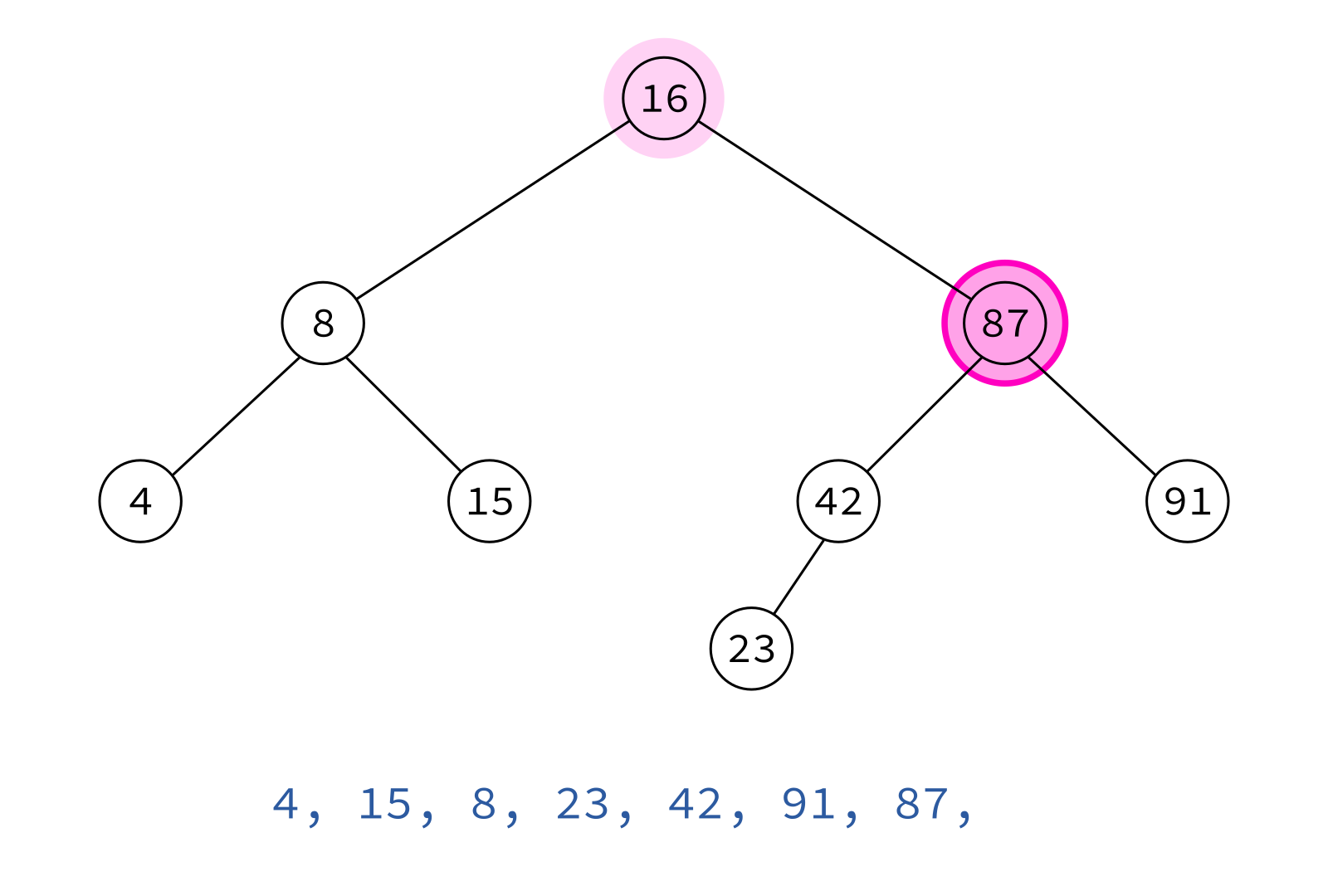
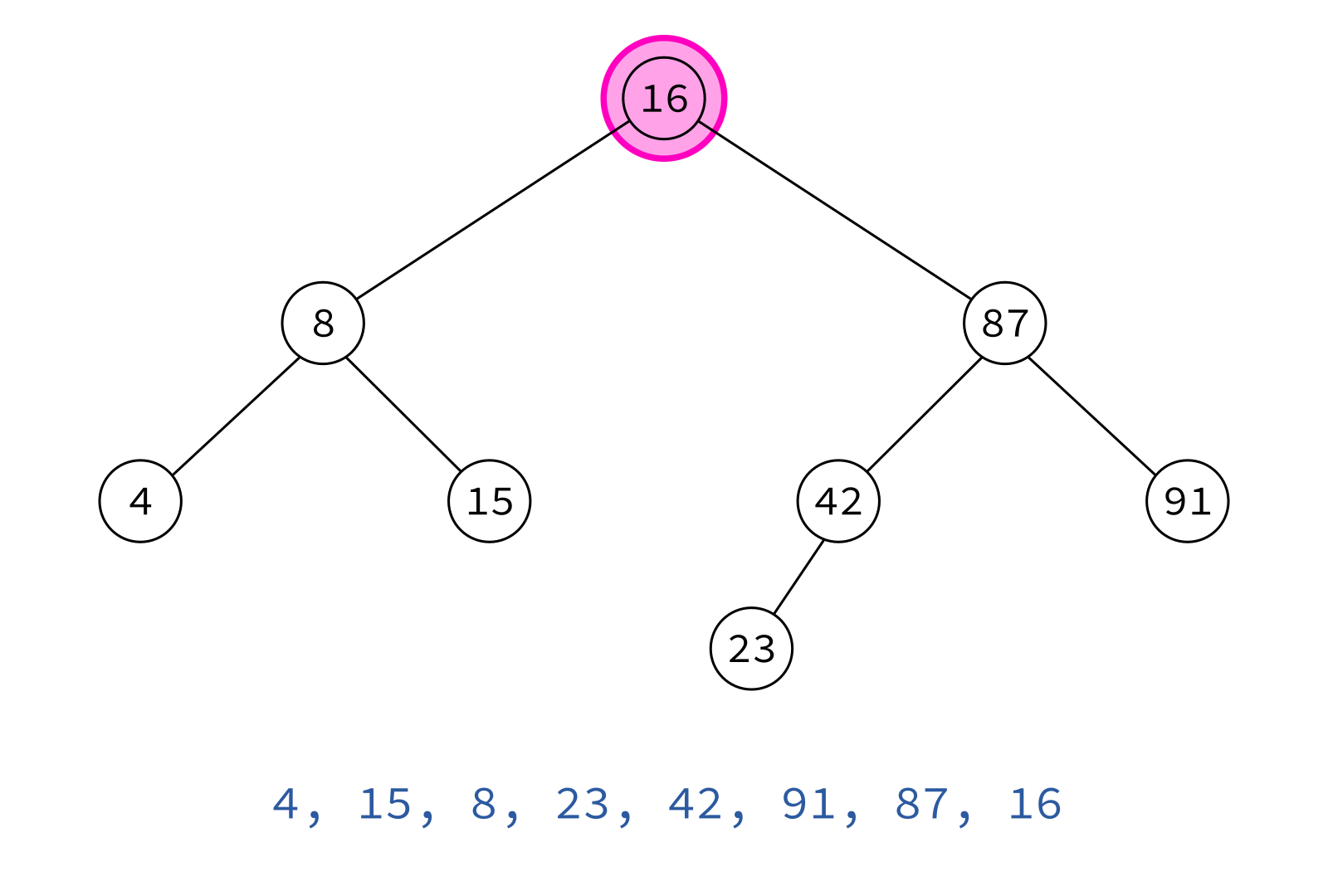
left, right, node

Postorder traversal

Typical use: Delete the tree.

If you delete keys in postorder, then you will only ever be removing nodes without children.

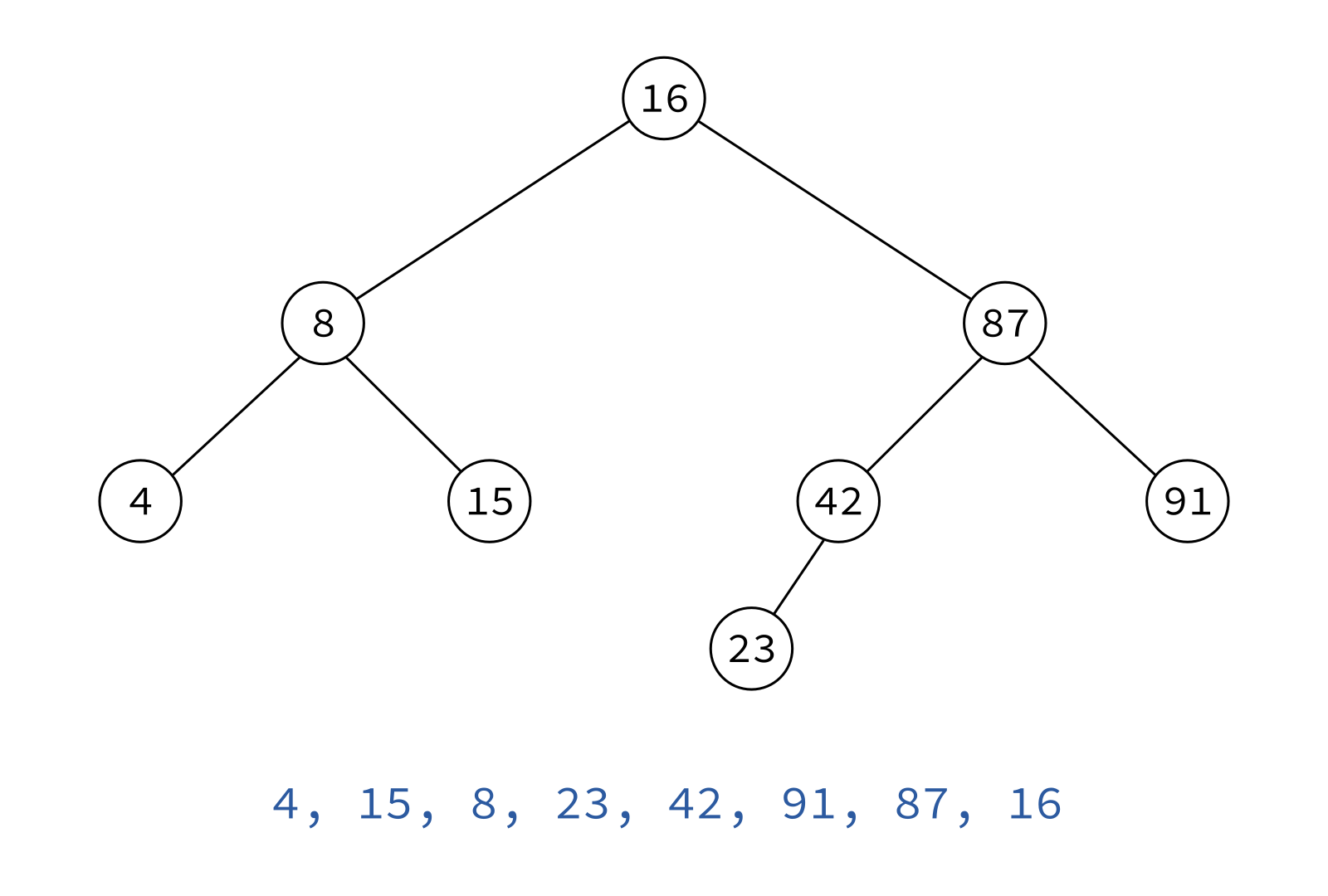
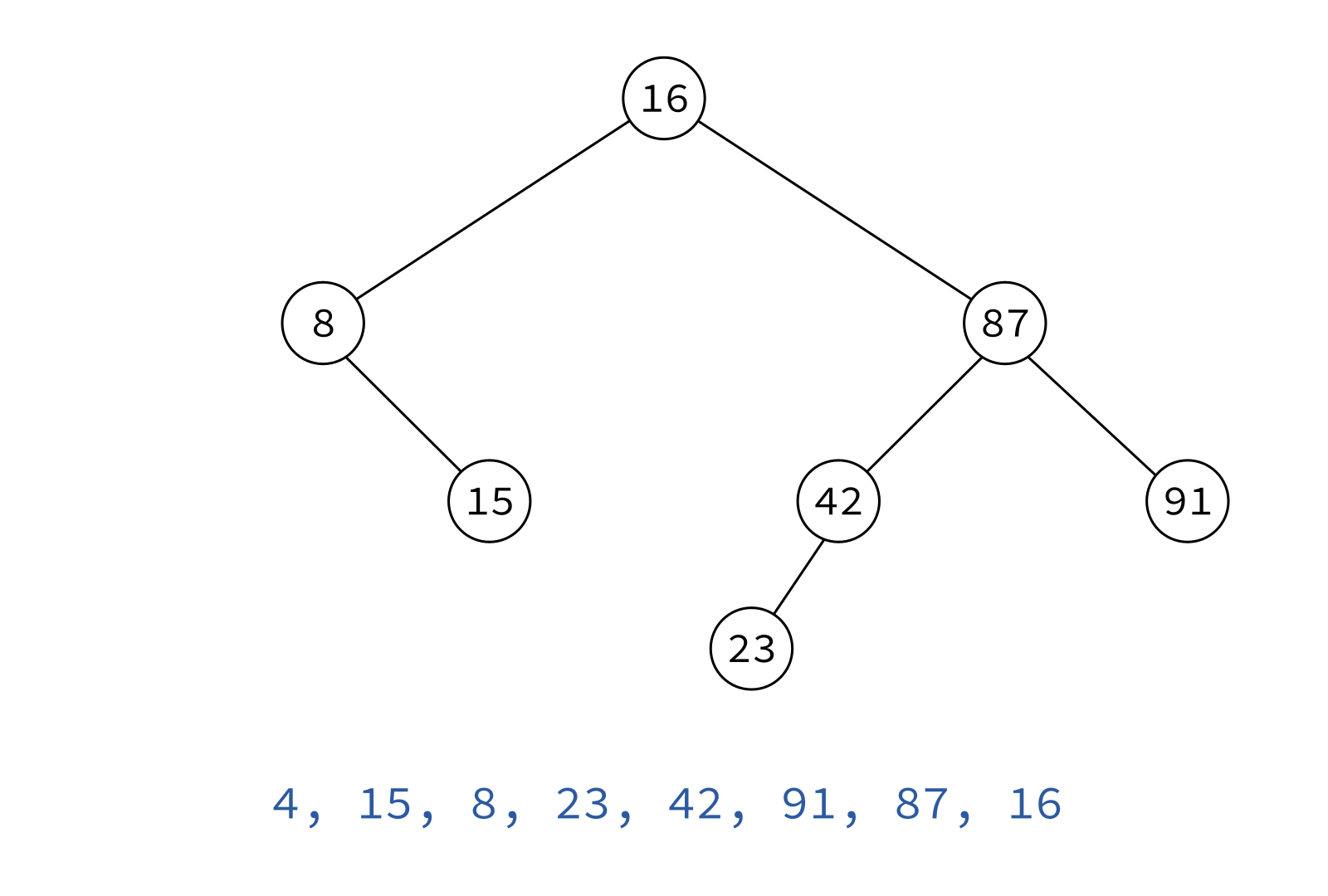
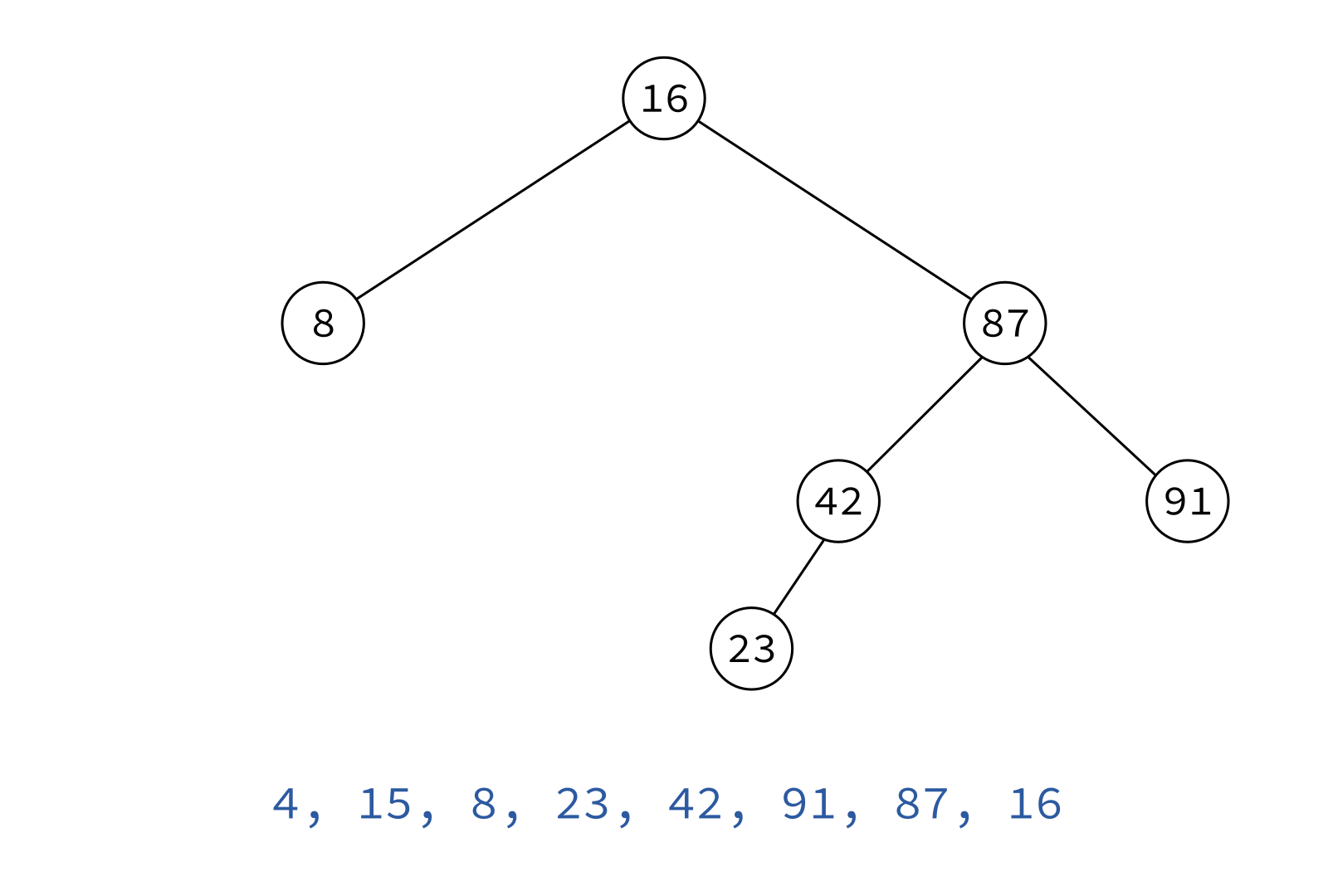
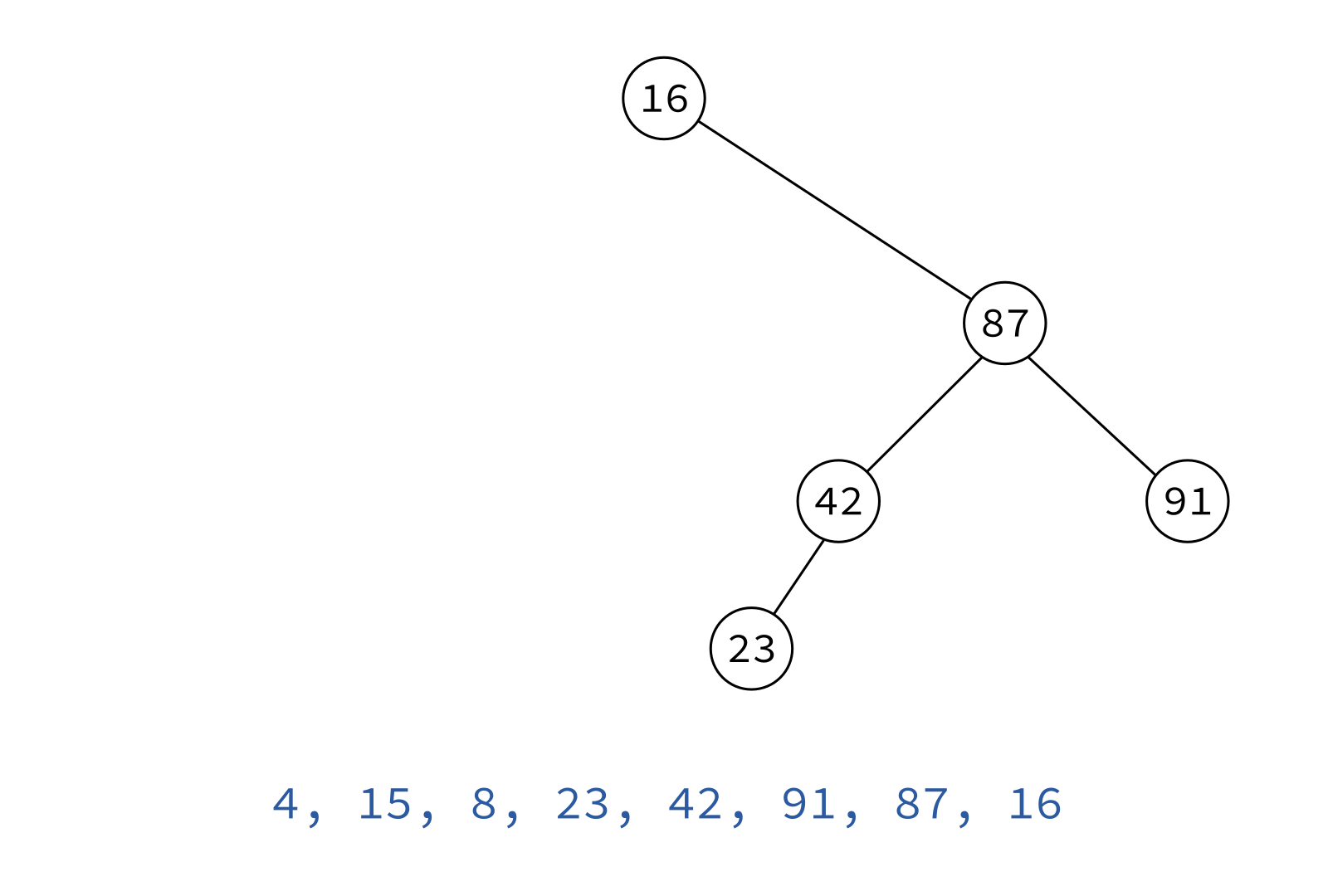
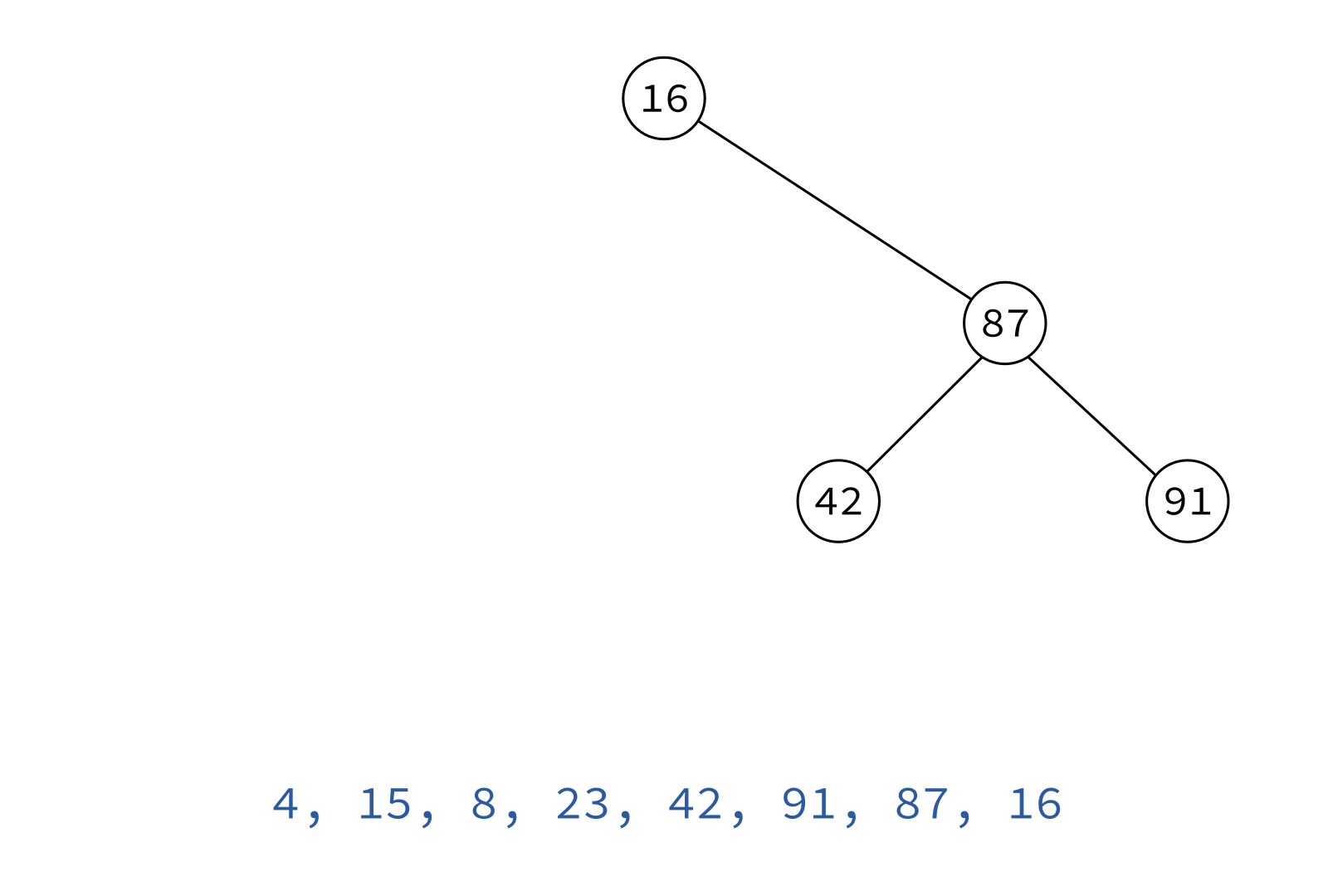
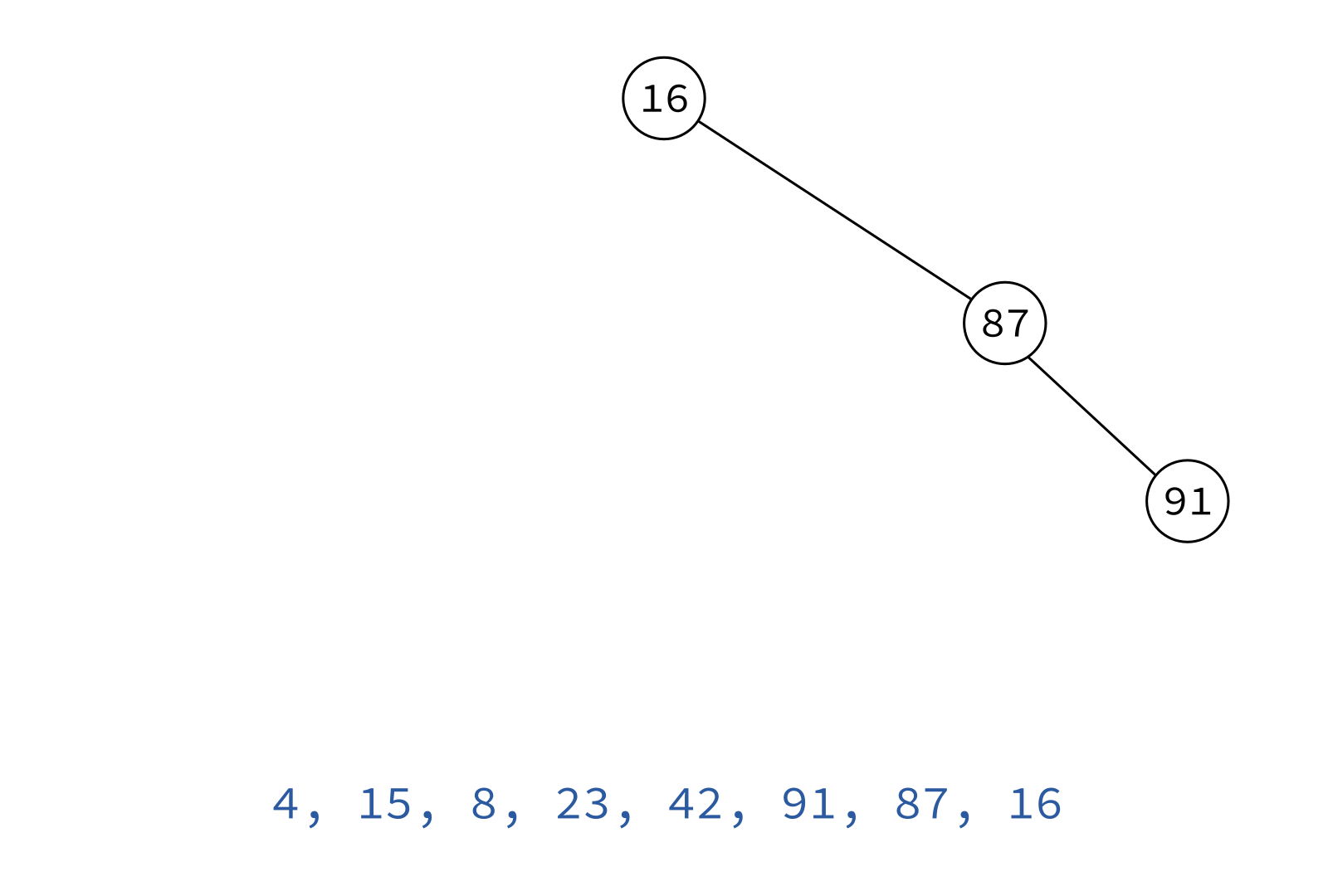
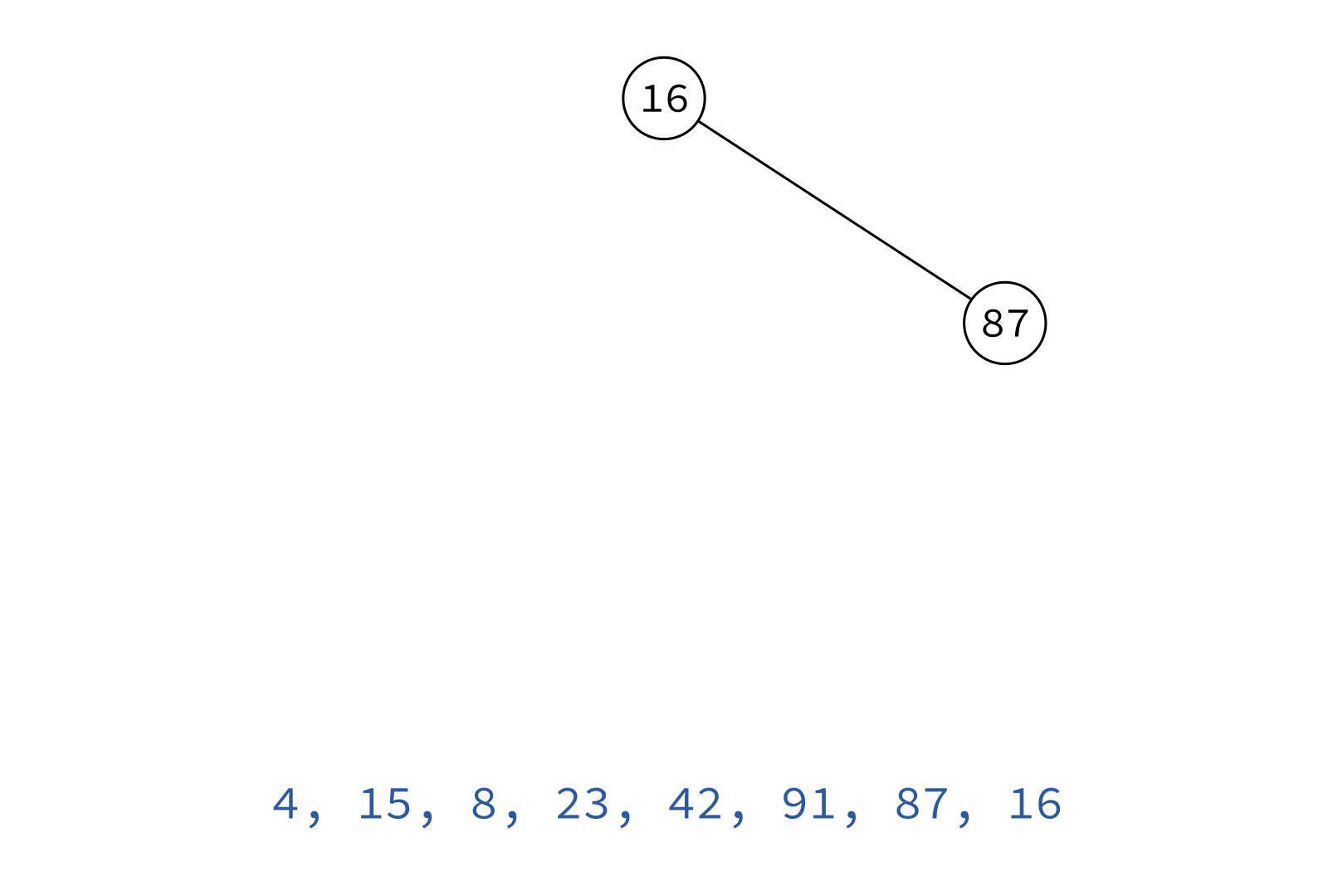
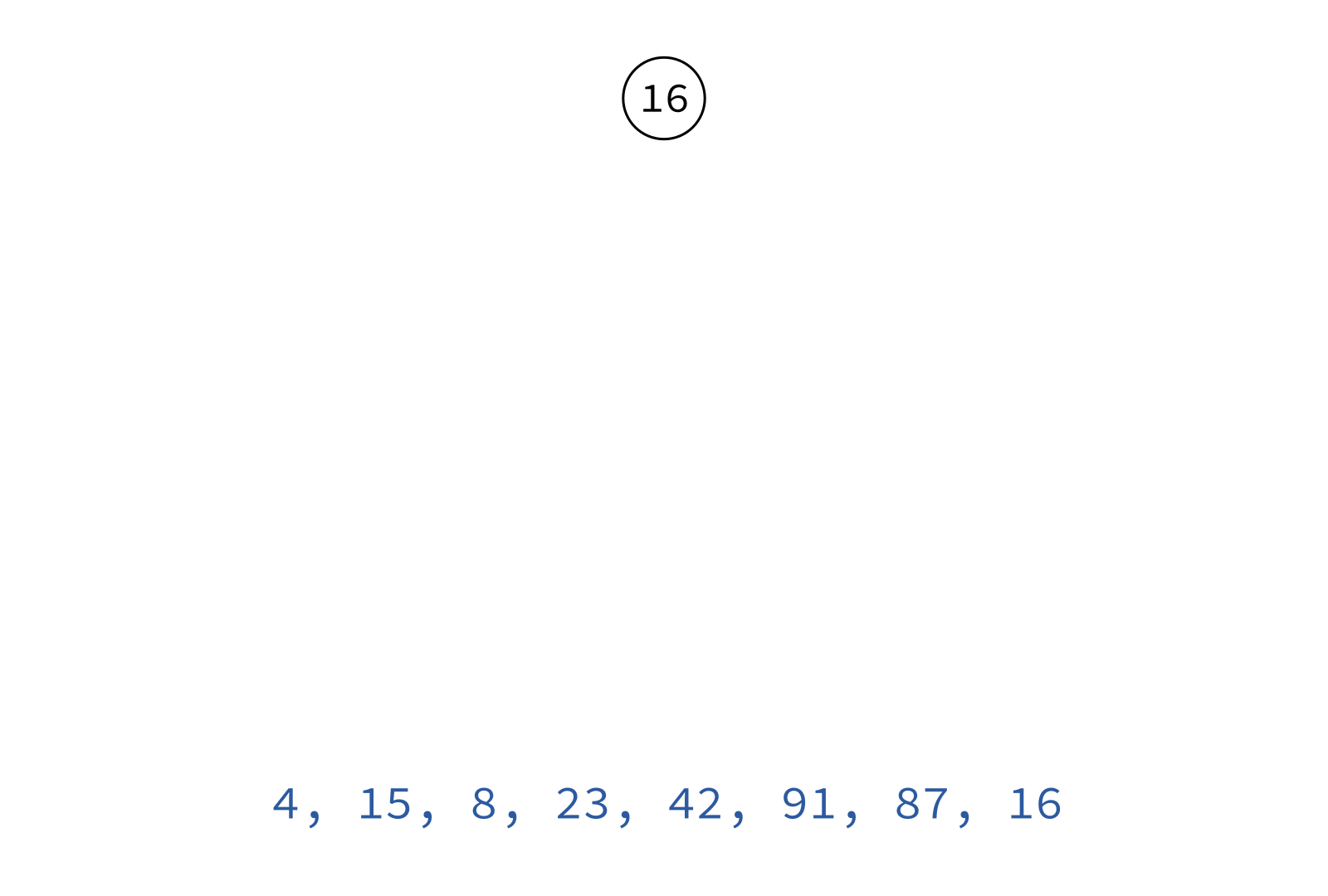
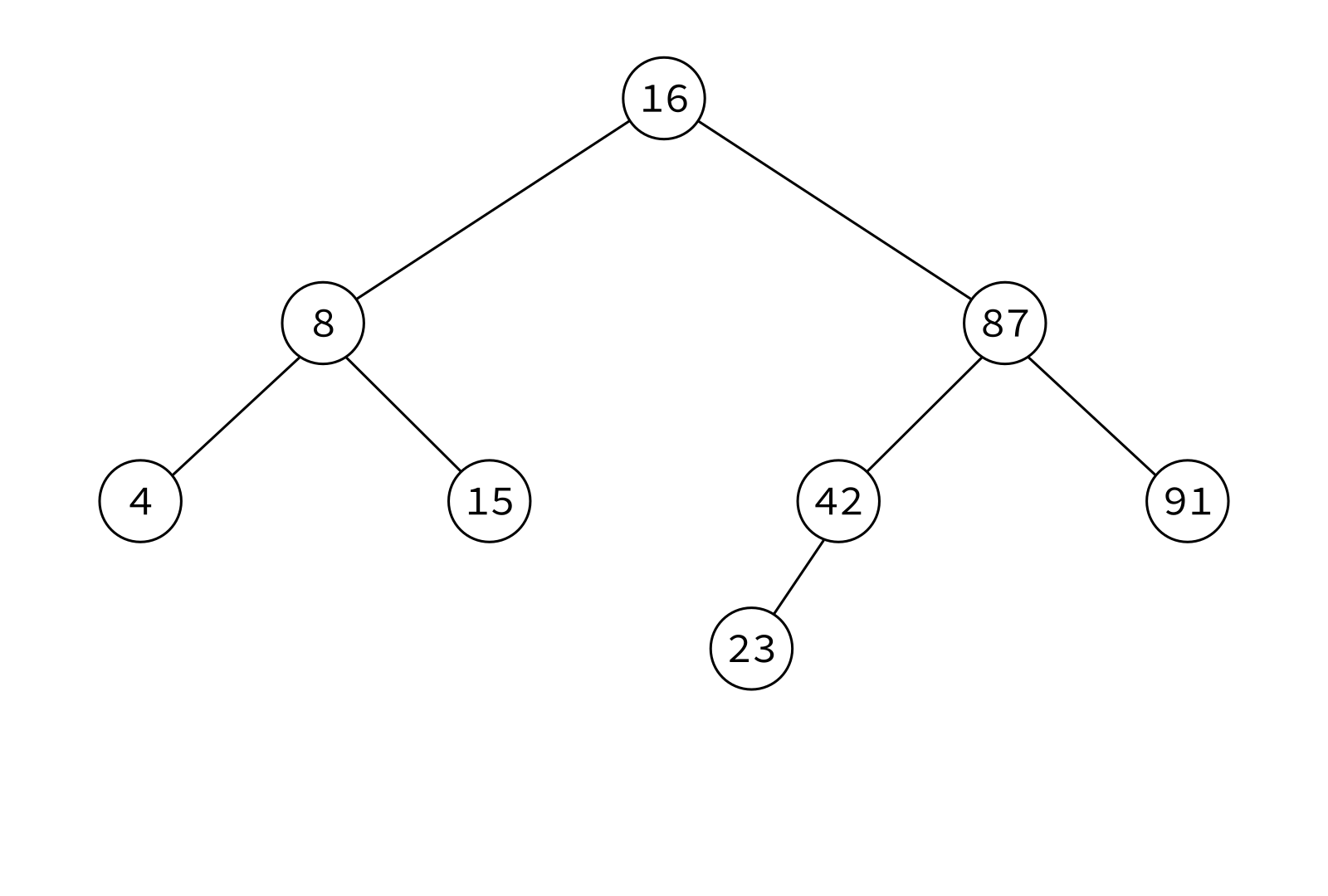
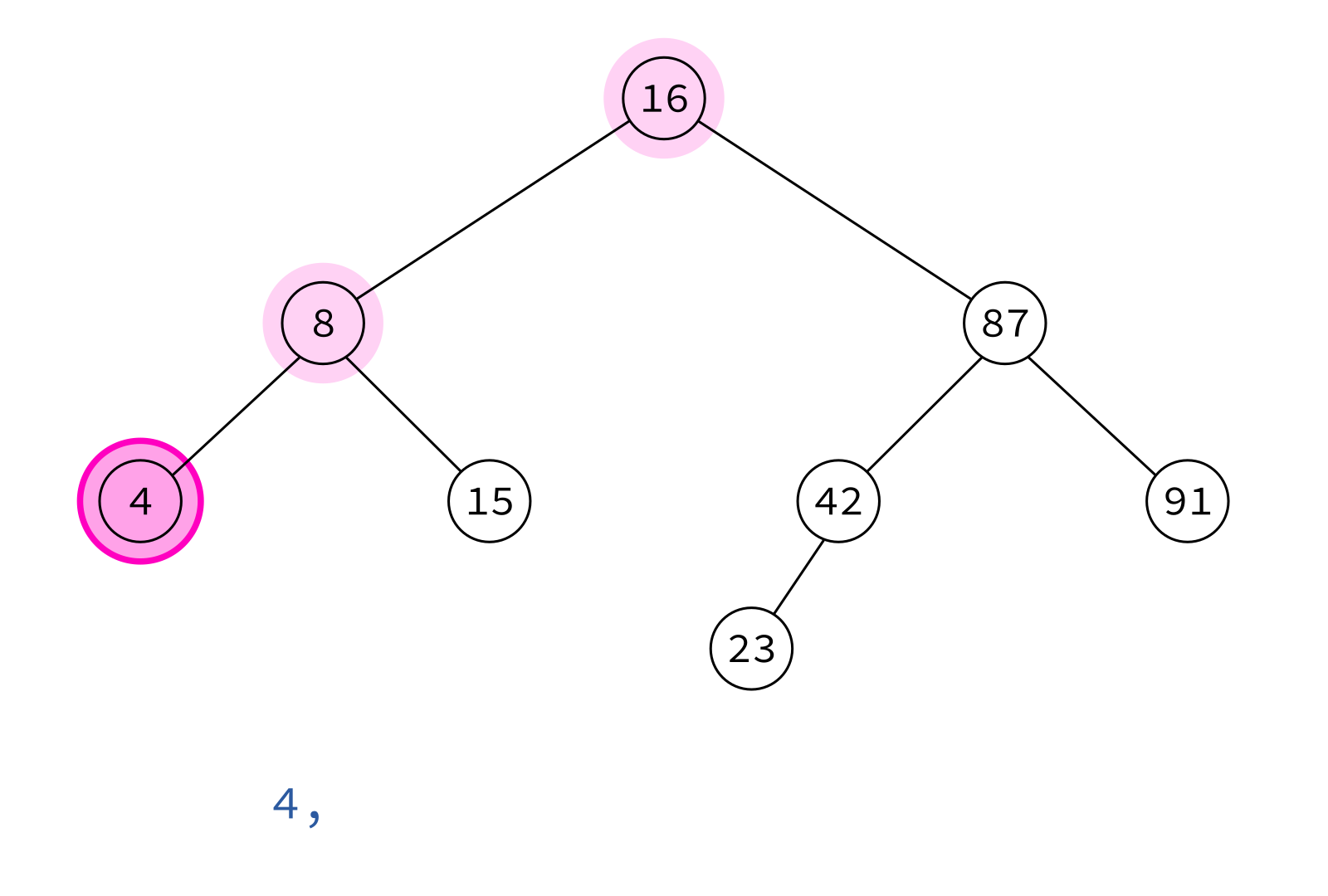
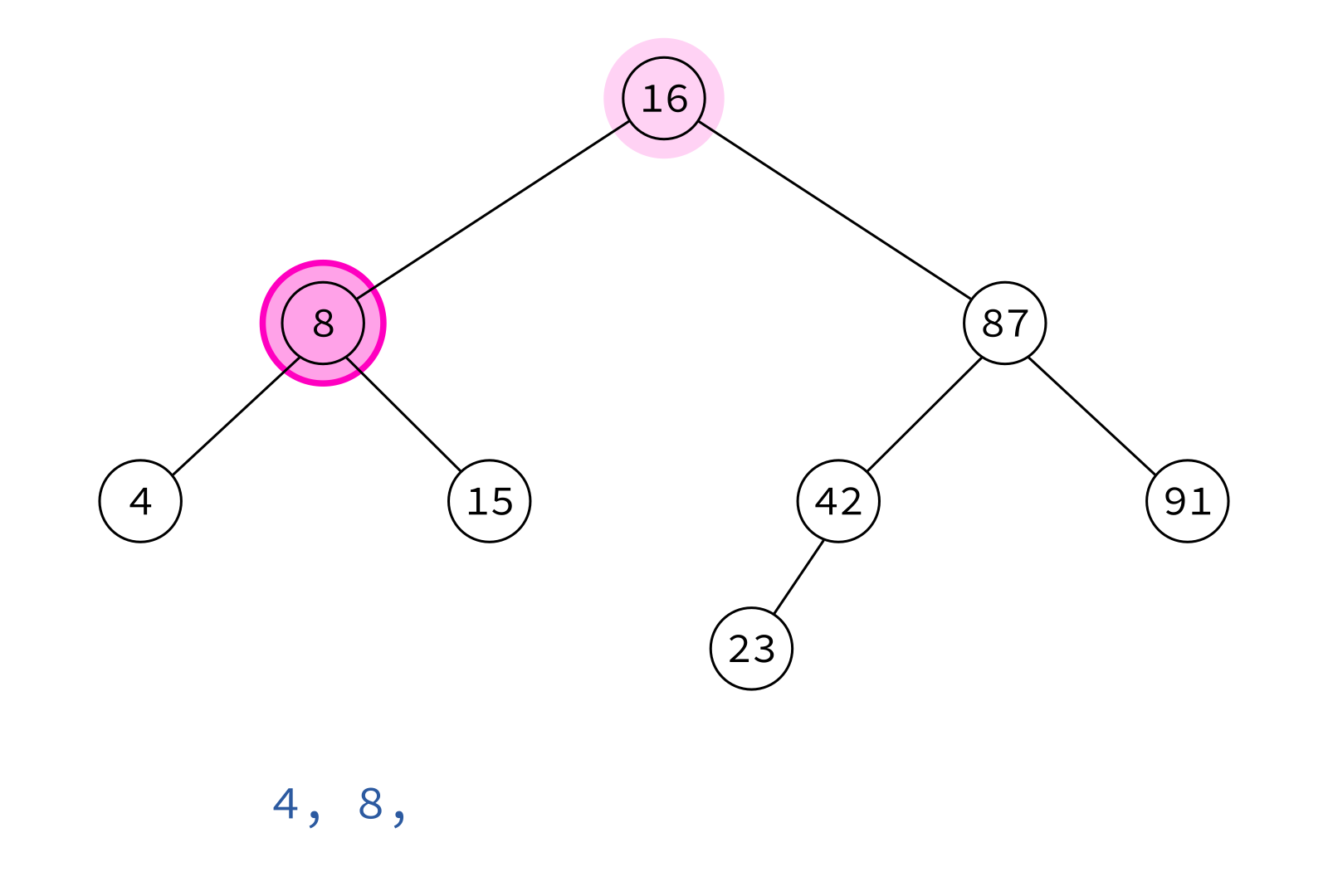
Inorder traversal

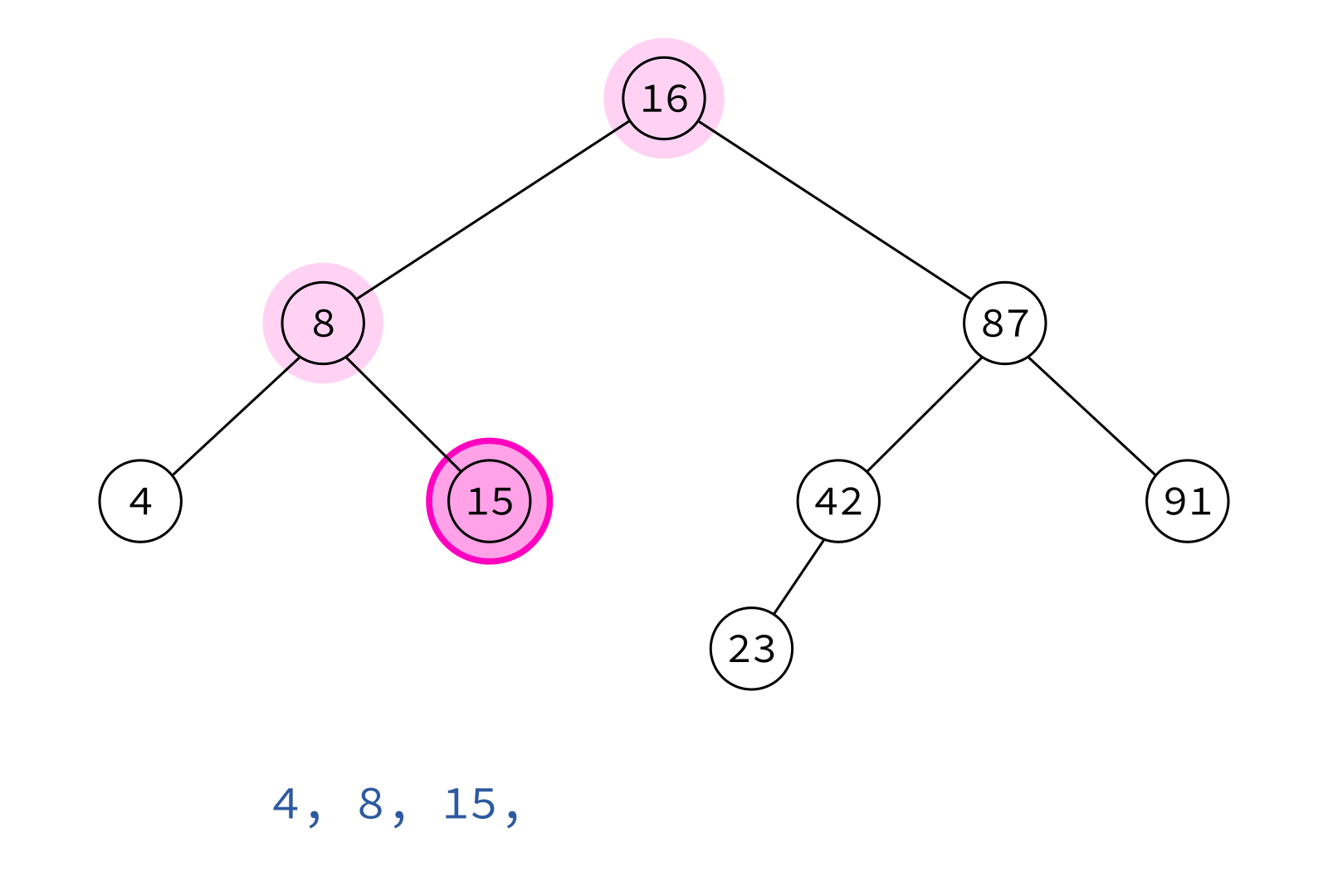
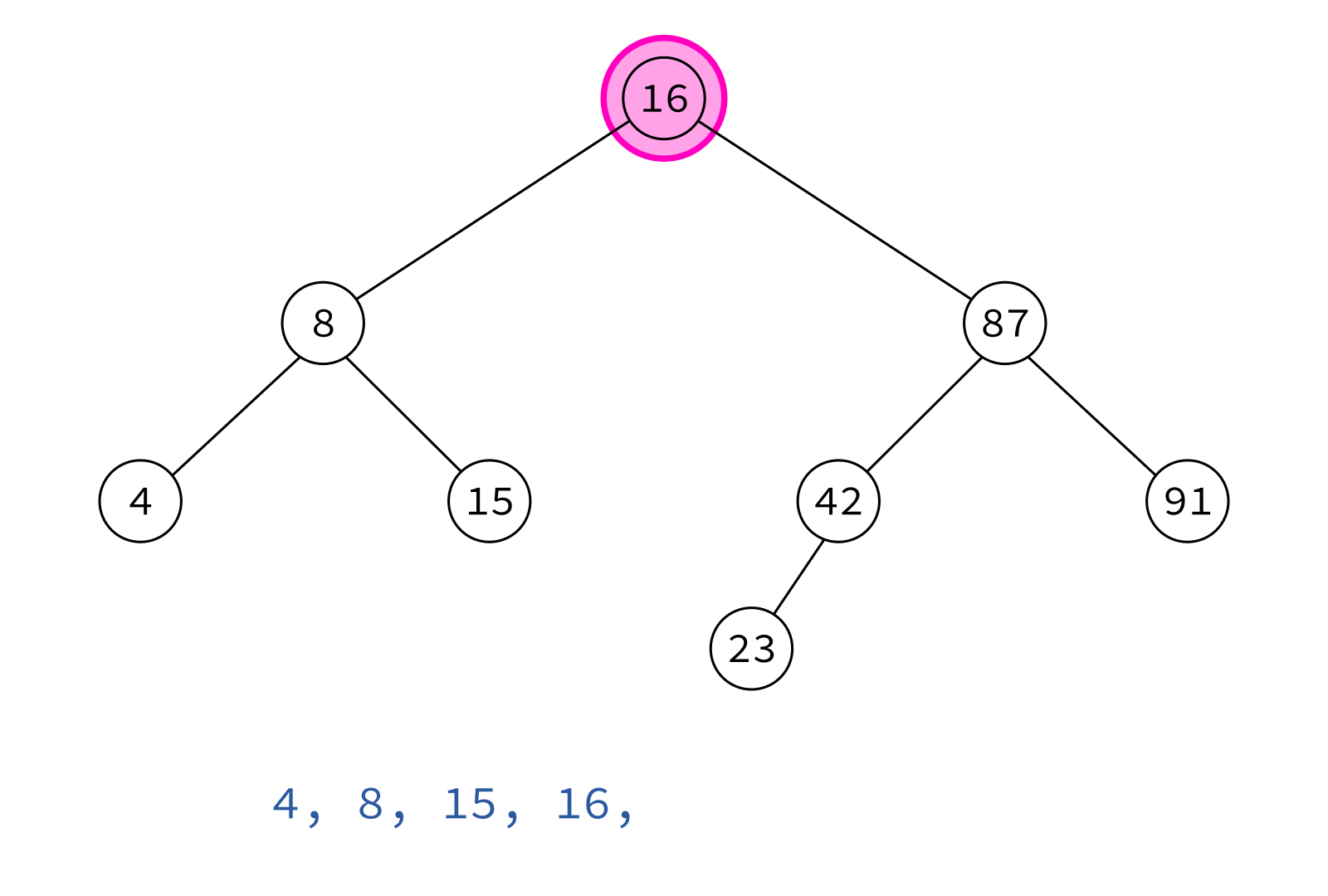
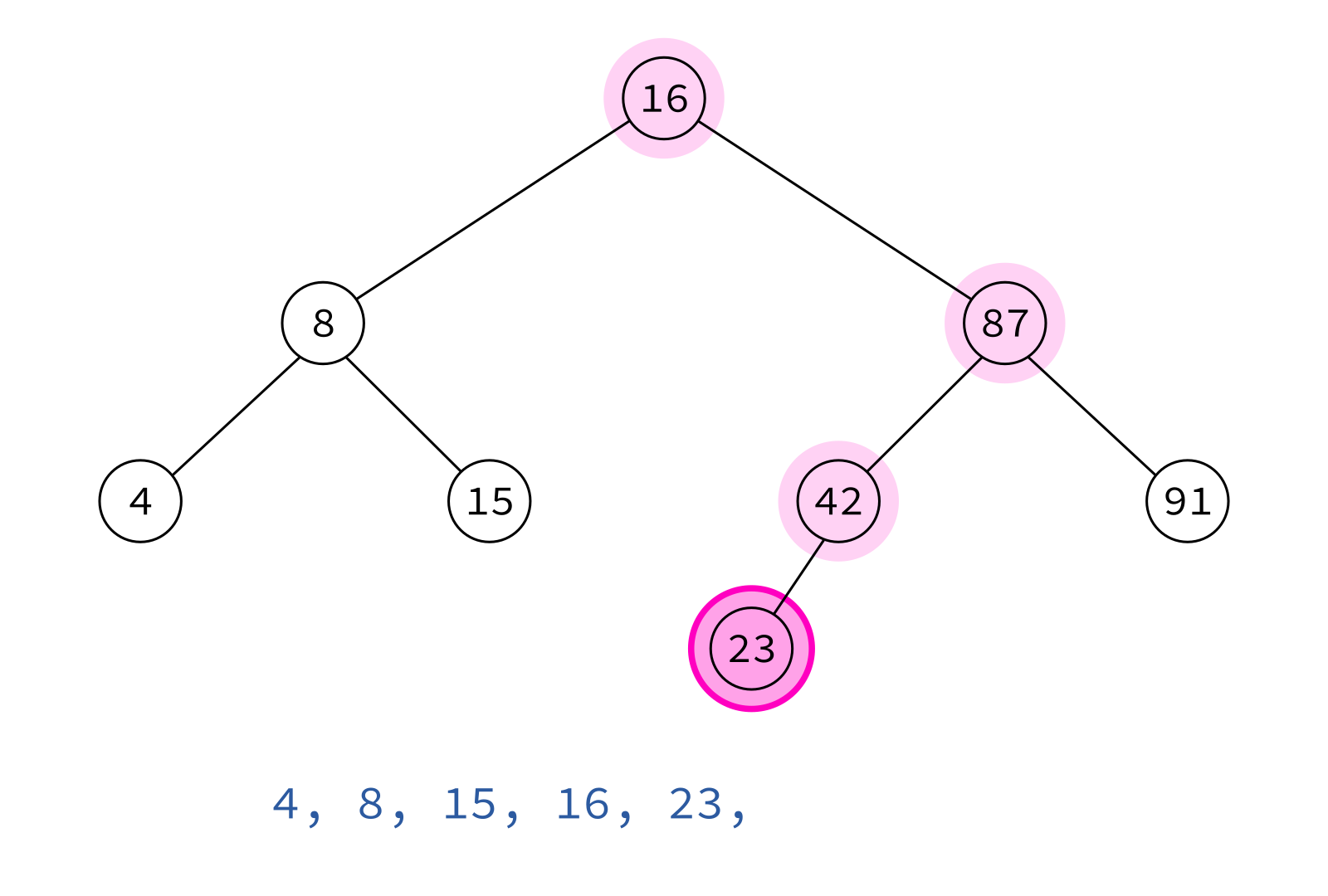
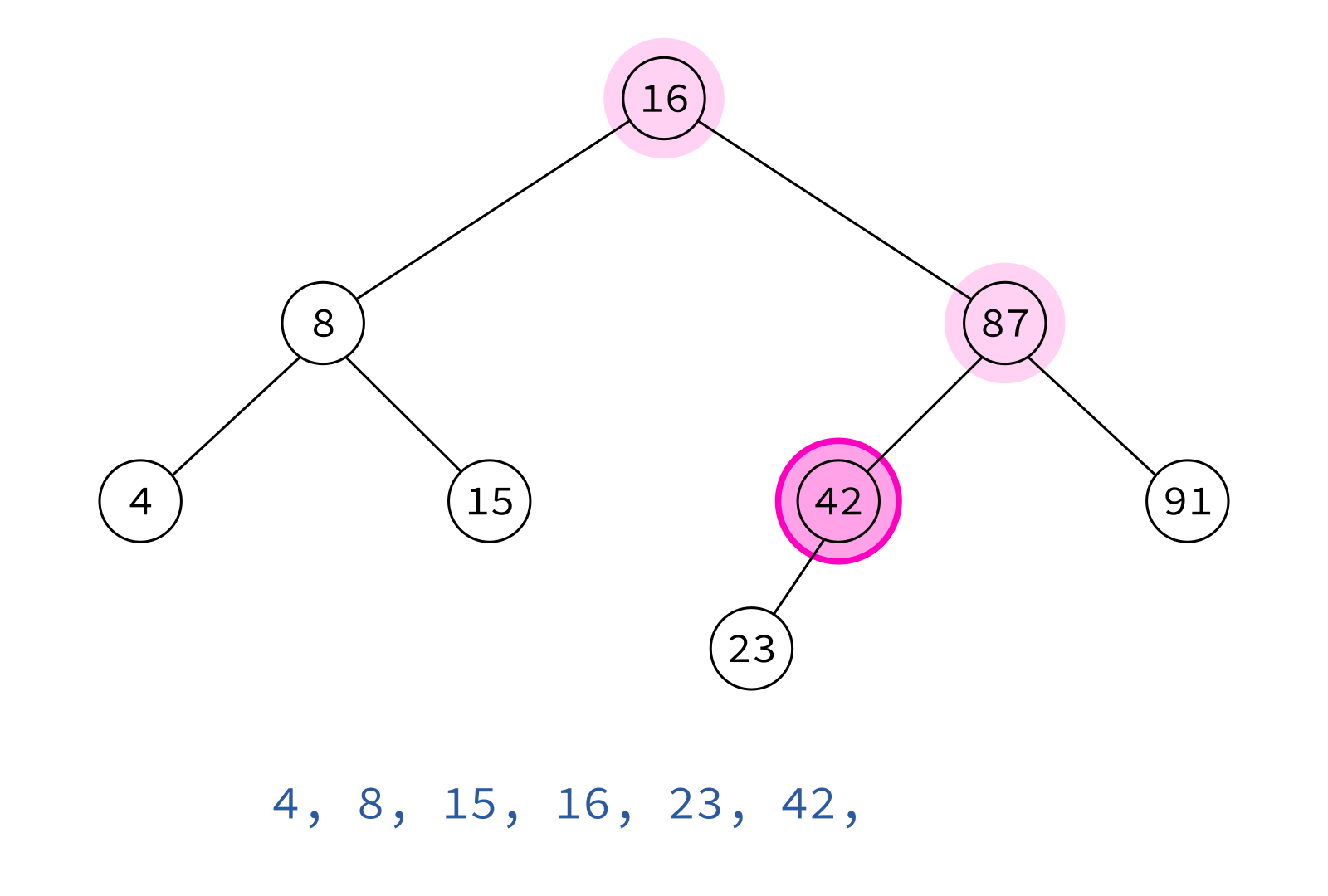
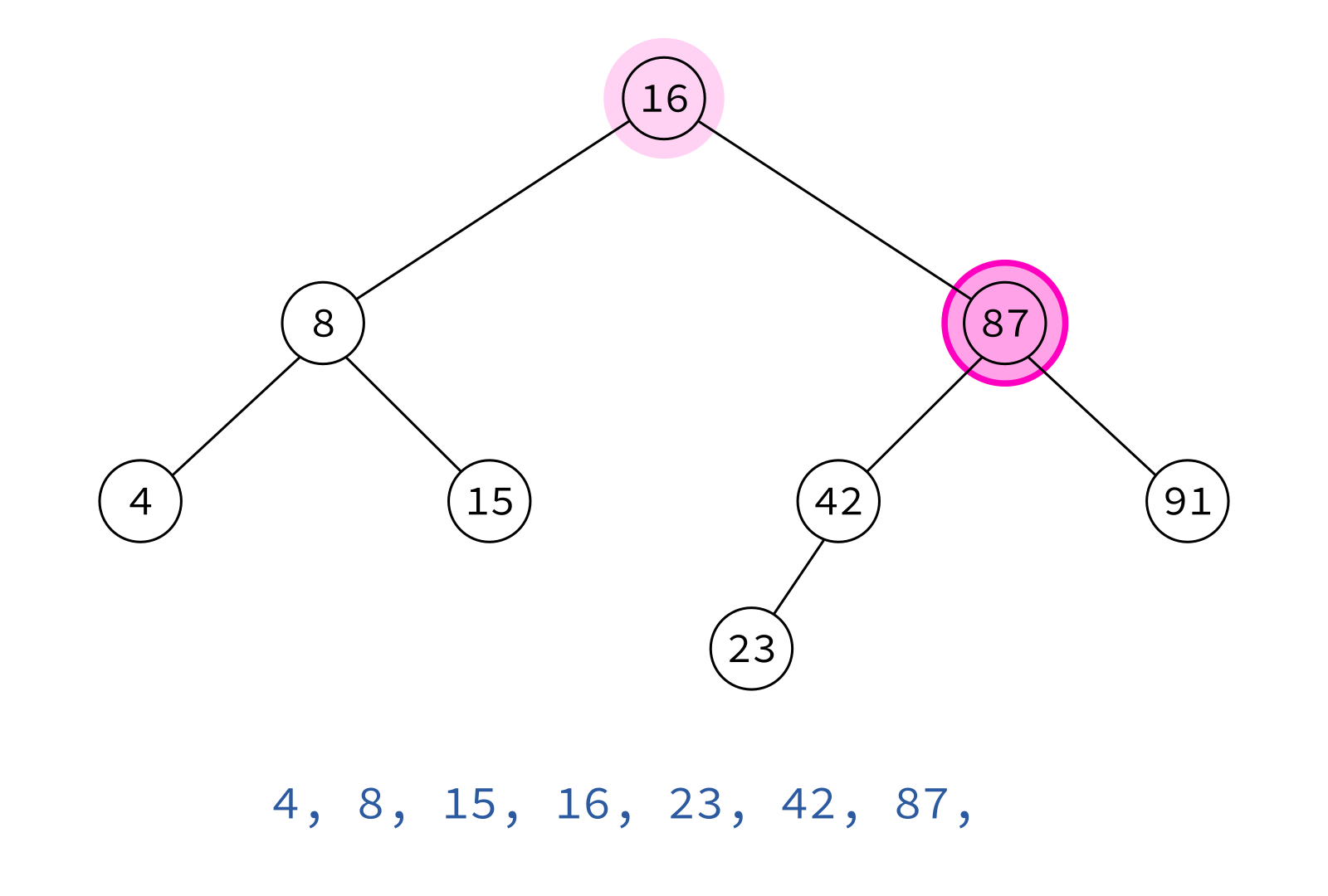
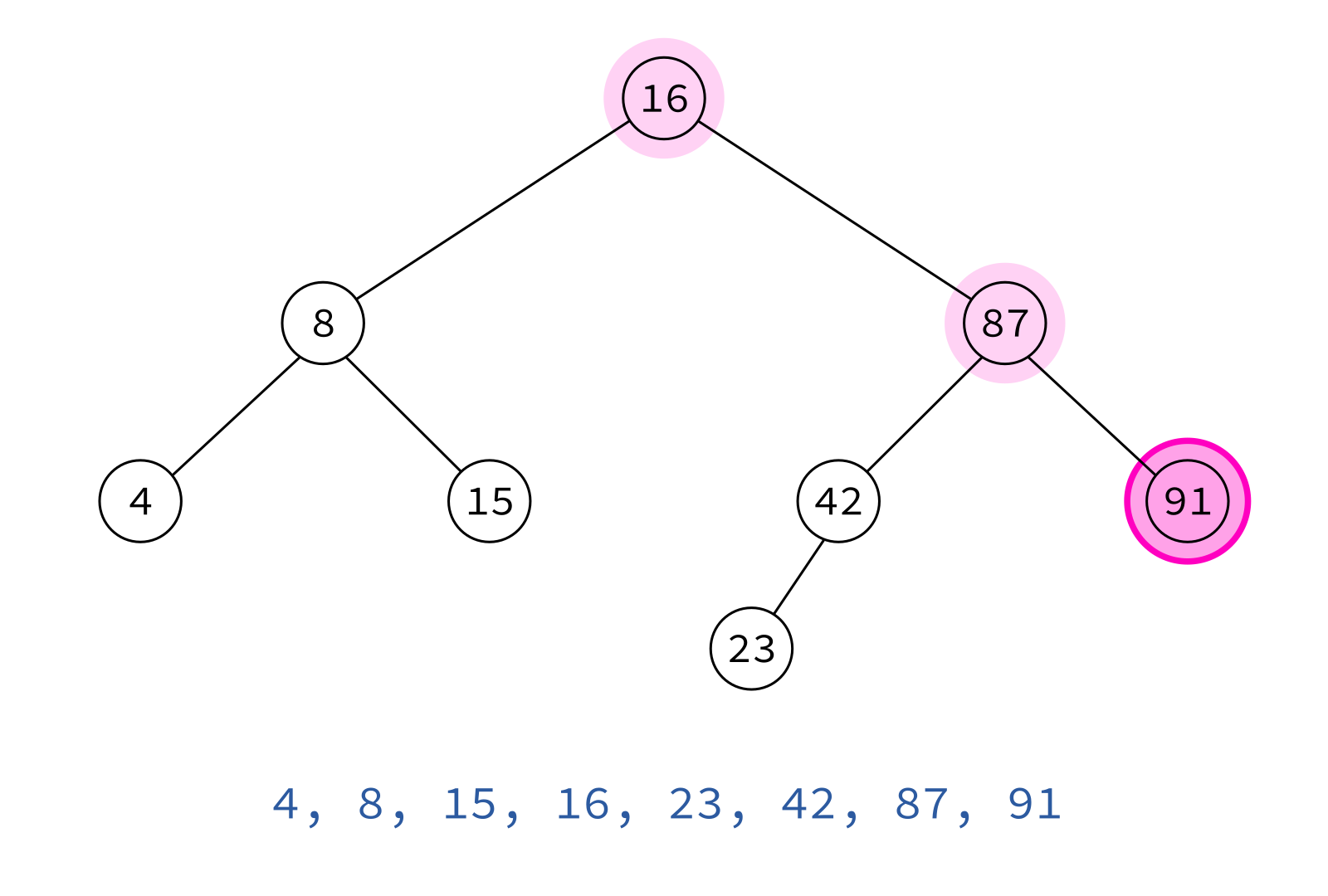
left, node, right

Inorder traversal

Typical use: Turn a BST into a sorted list of keys.