Lecture 16
Mergesort
MCS 275 Spring 2021
Emily Dumas
Lecture 16: Mergesort
Course bulletins:
- Starting with Quiz 6, you will have 48 hours for quizzes (Noon Sunday to Noon Tuesday).
- Project 2 description updated with sample data and modules policy.
- Project 2 due 6pm CST Friday, February 26.
- Check out the recursion sample code.
- Worksheet 7 will explore recursive maze solver / generator in more depth.
Plan
- Discuss the theory of
- Divide and conquer
- Sorting
- Mergesort
- Implement mergesort
Divide and conquer
A strategy that often involves recursion.
- Split a problem into parts.
- Solve for each part.
- Merge the partial solutions into a solution of the original problem.
Not always possible or a good idea. It only works if merging partial solutions is easier than solving the entire problem.
Comparison sort
Suppose you have a list of objects that can be compared with ==, >, <.
You'd like to reorder them in increasing order.
This problem is called comparison sort. There are many solutions.
Mergesort
A divide-and-conquer solution to comparison sort.
It is a fast solution, often used in practice.
Key: It is pretty easy to take two sorted lists and merge them into a single sorted list.
So, let's divide our list into halves, sort each one (recursively), then merge them.
Now we'll formalize this.
mergesort:
Input: list L whose elements support comparison.
Goal: reorder the elements of L in place to achieve sorted order.
- If
Lhas 0 or 1 elements, it is already sorted. Do nothing. - Otherwise, copy the first half of
Linto a new listL1, and the rest intoL2. - Use recursive calls to sort
L1andL2(in place). - Use
merge_sorted_liststo mergeL1andL2intoL.
Mergesort example

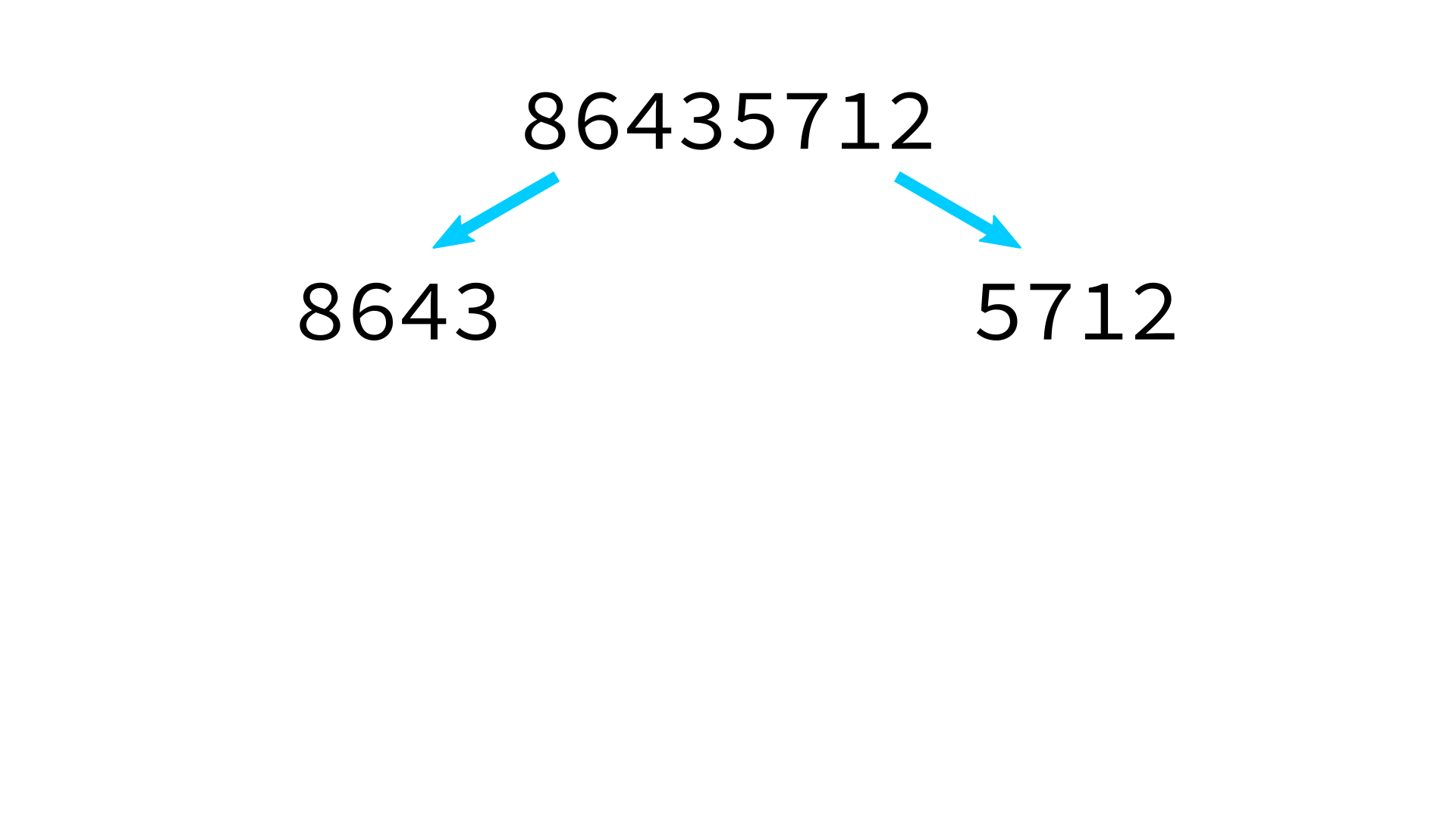
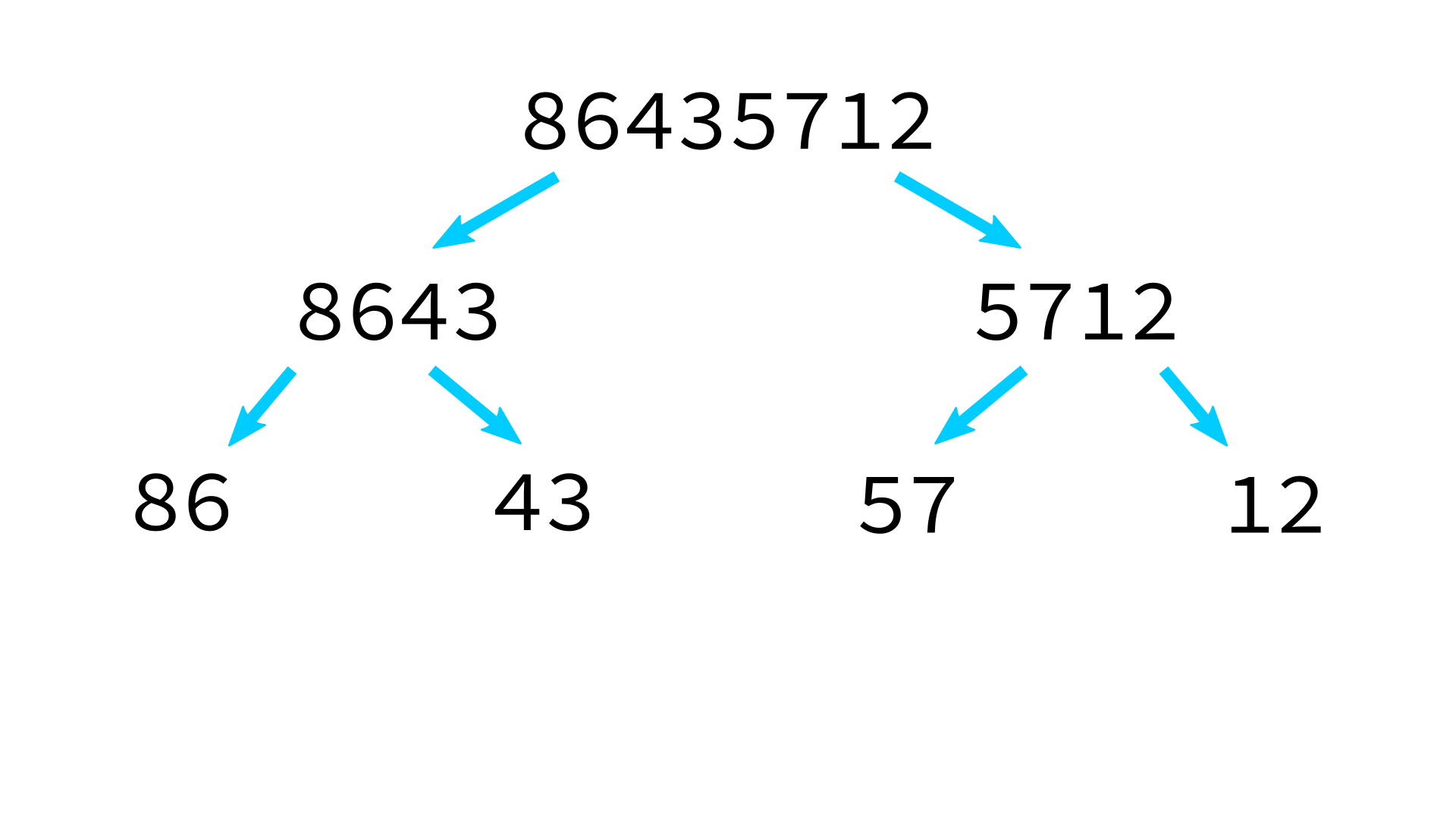
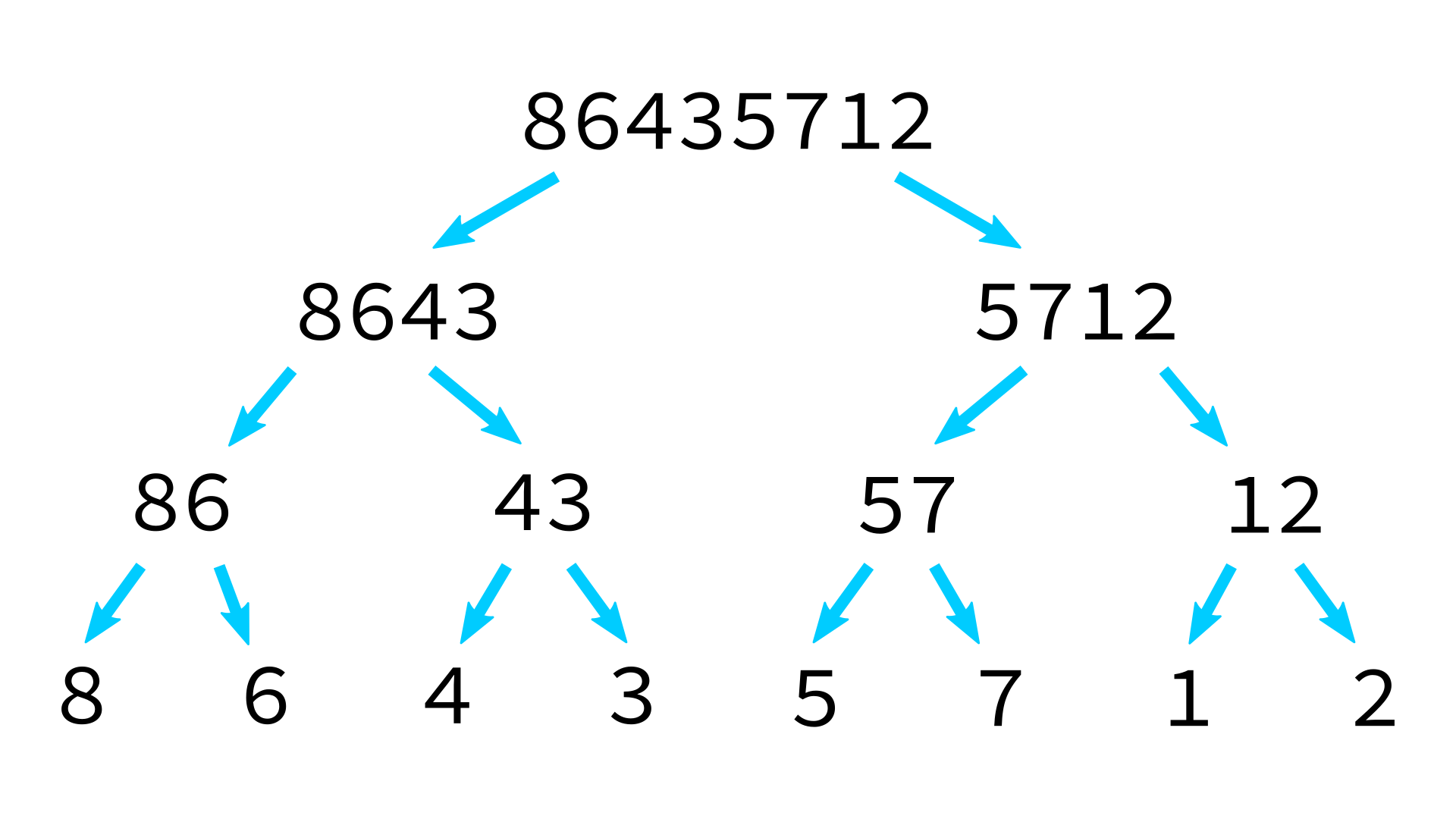
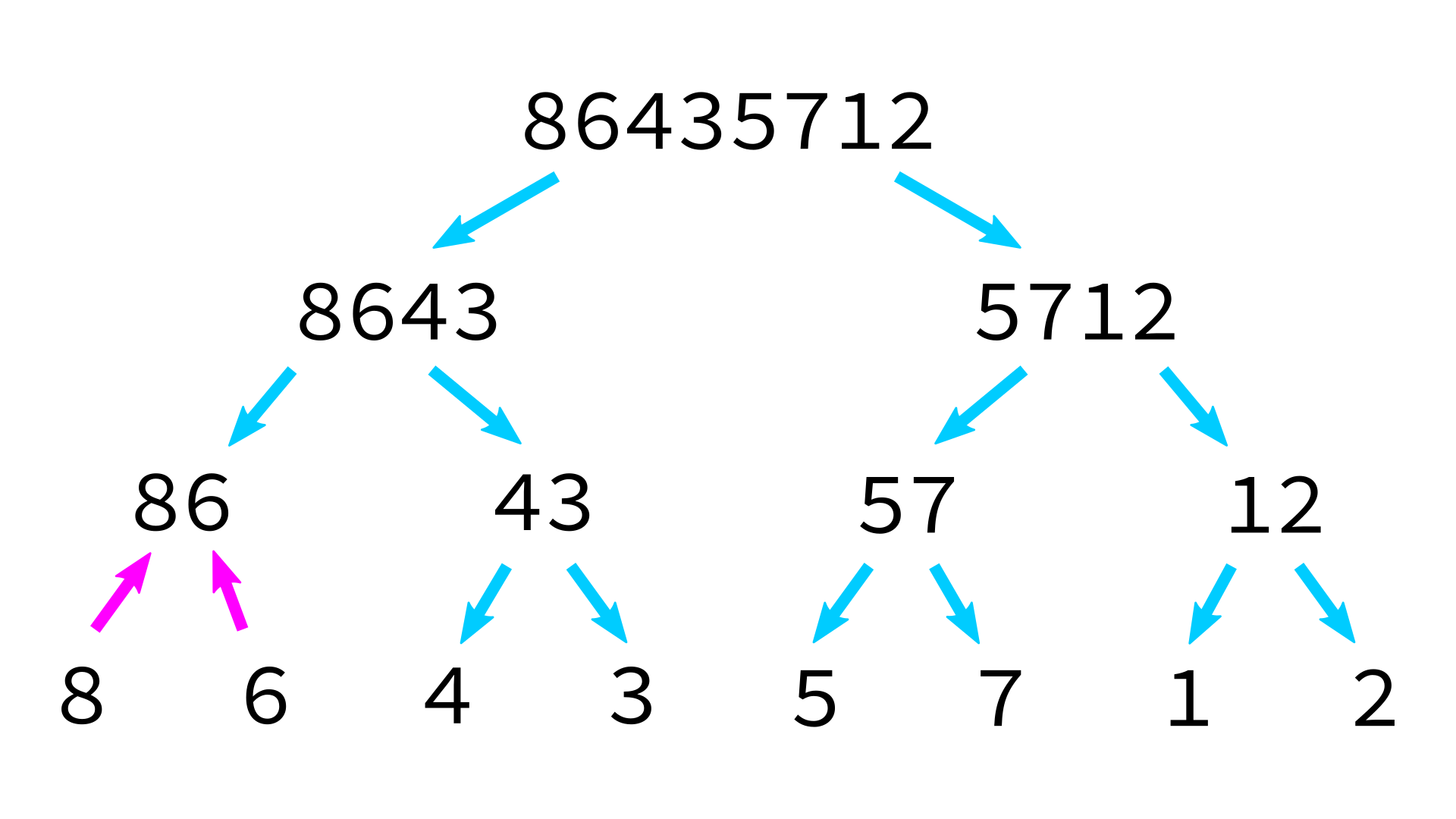
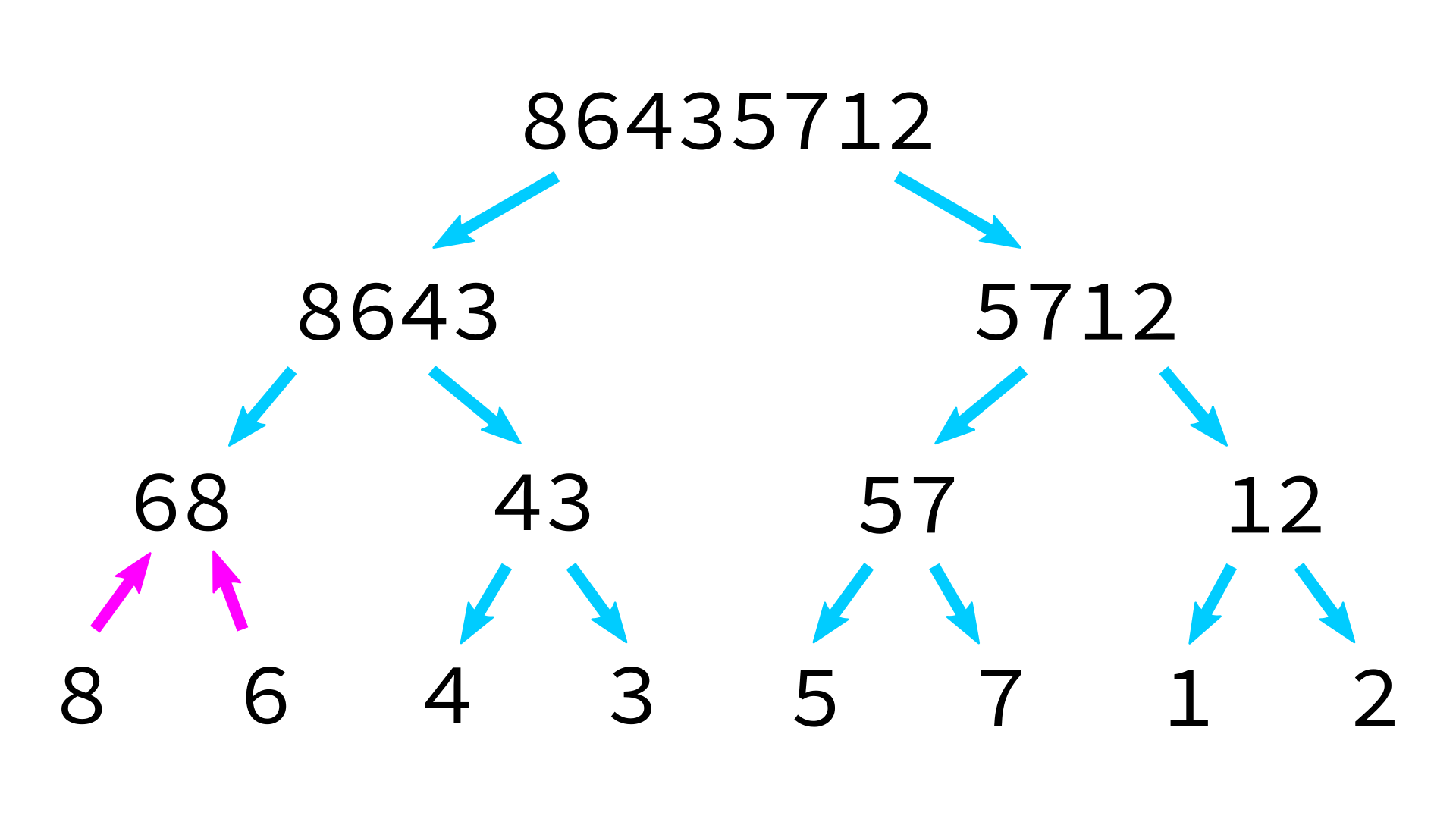
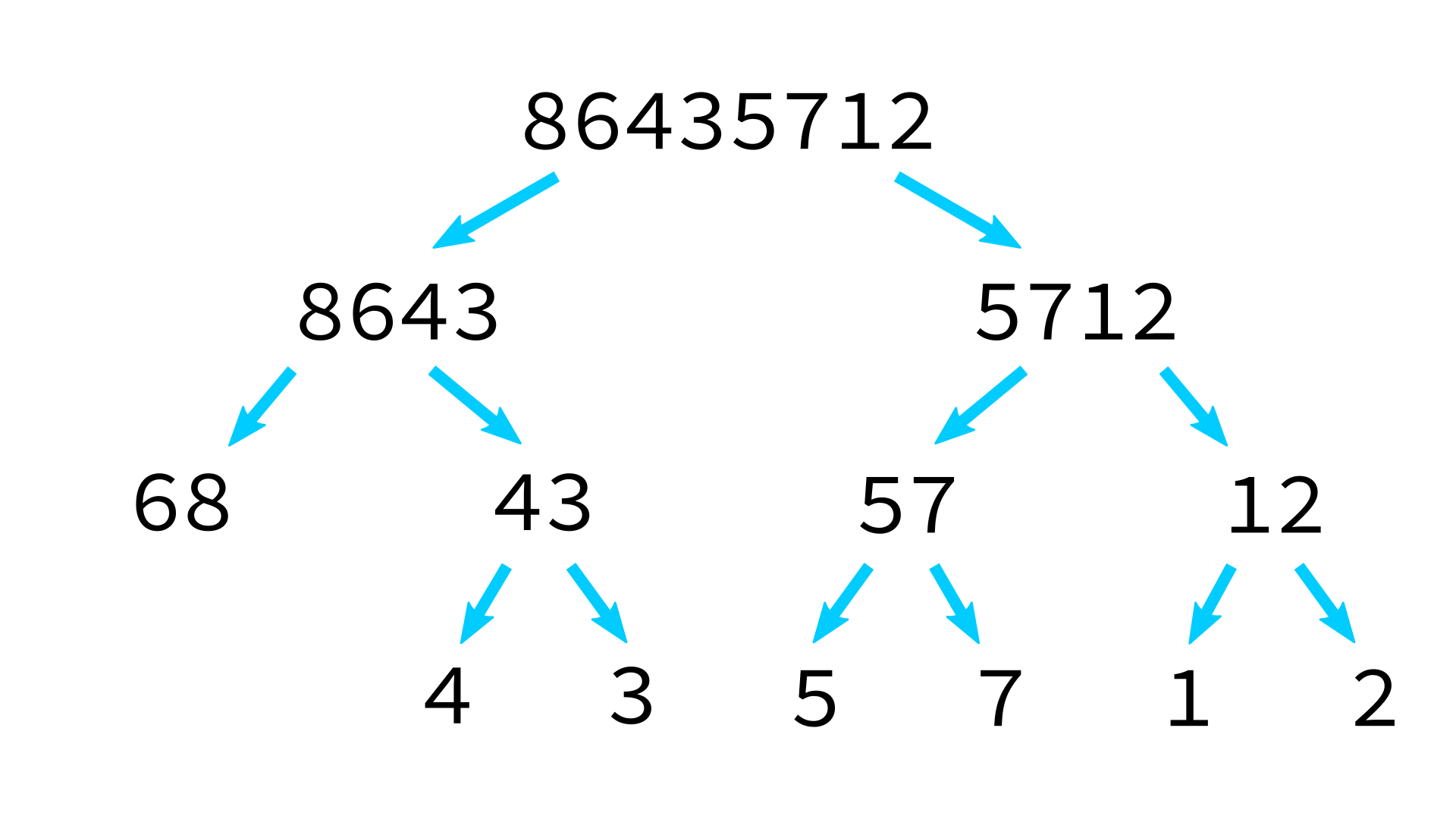
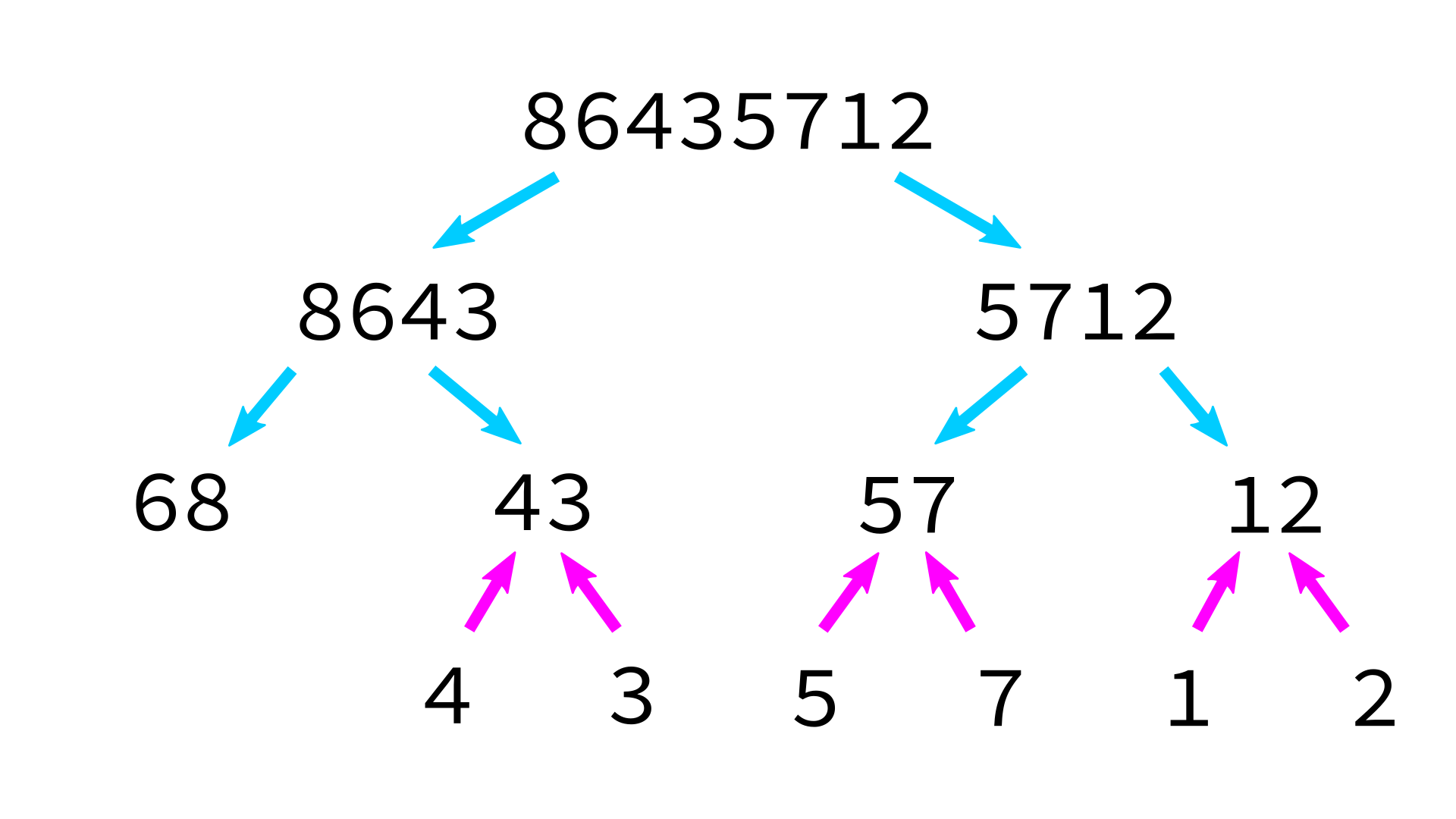
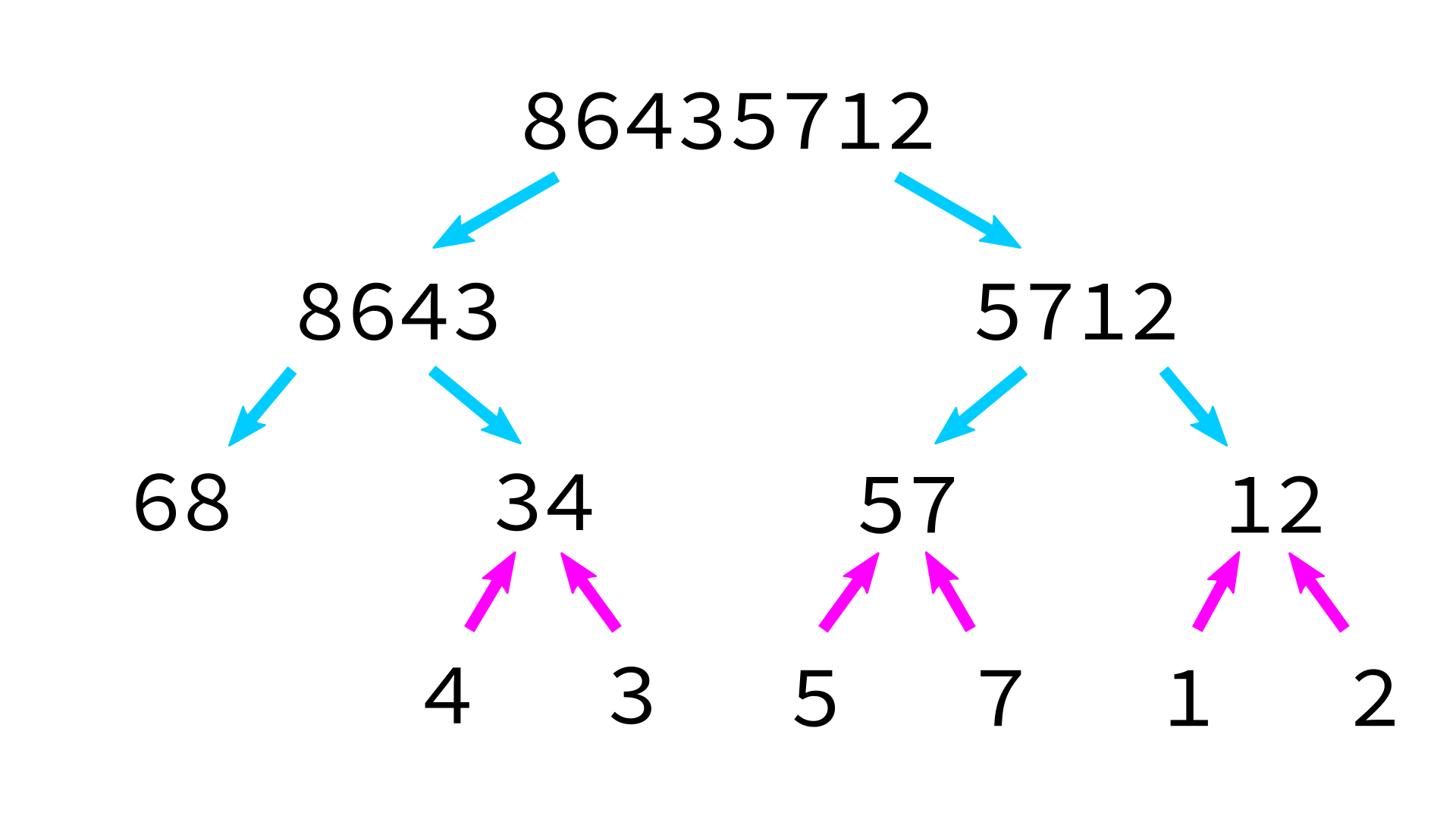
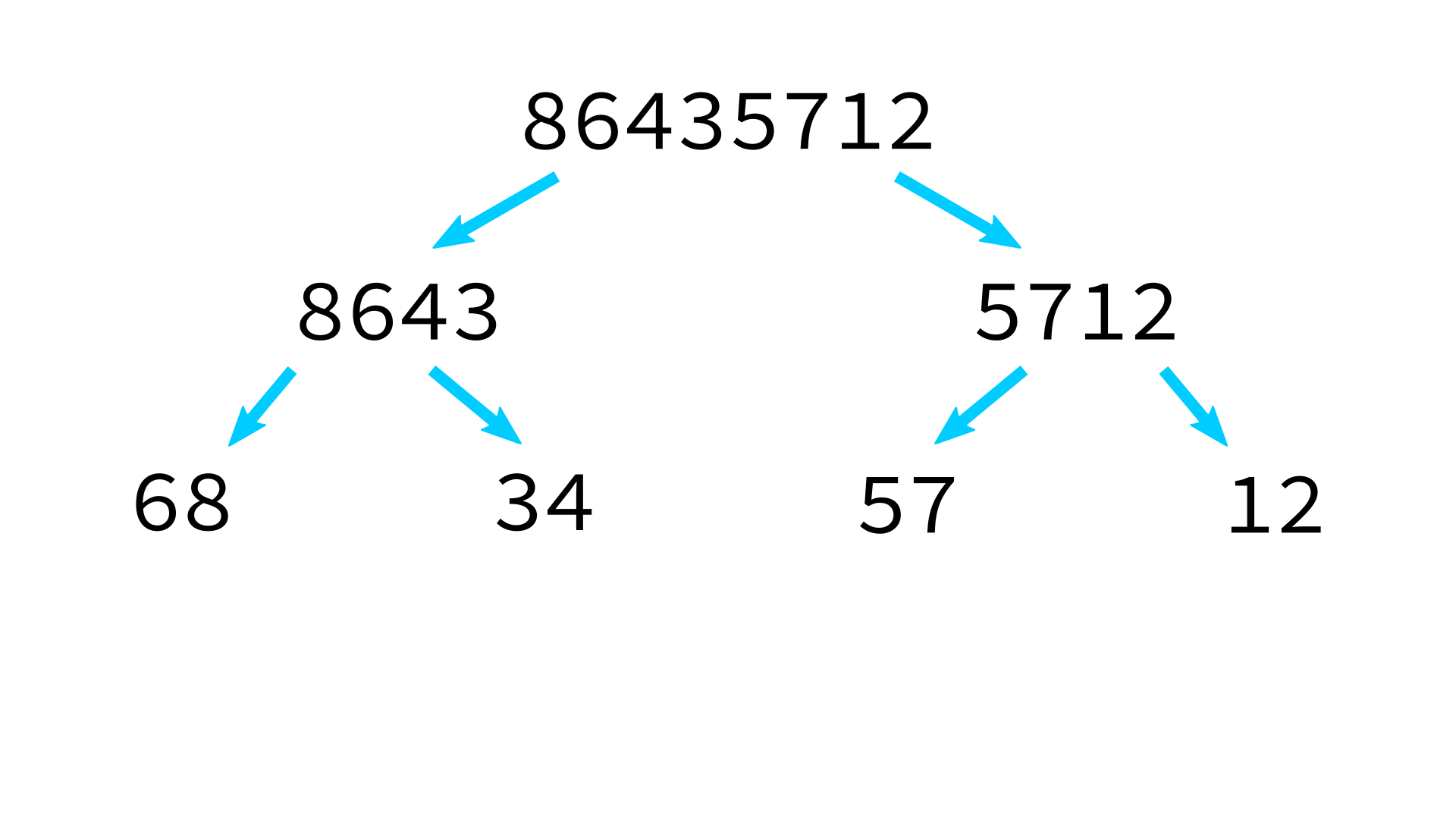
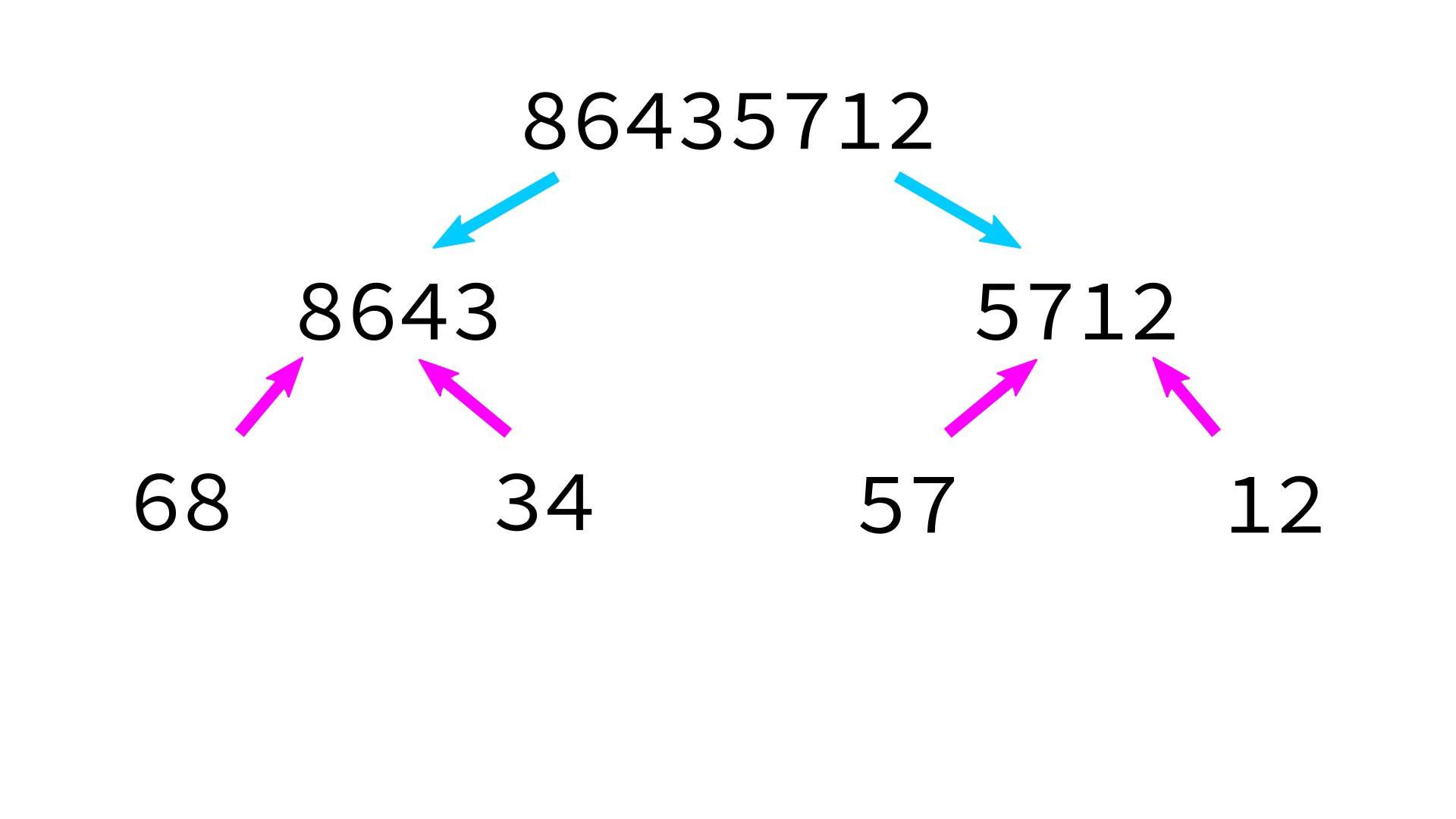
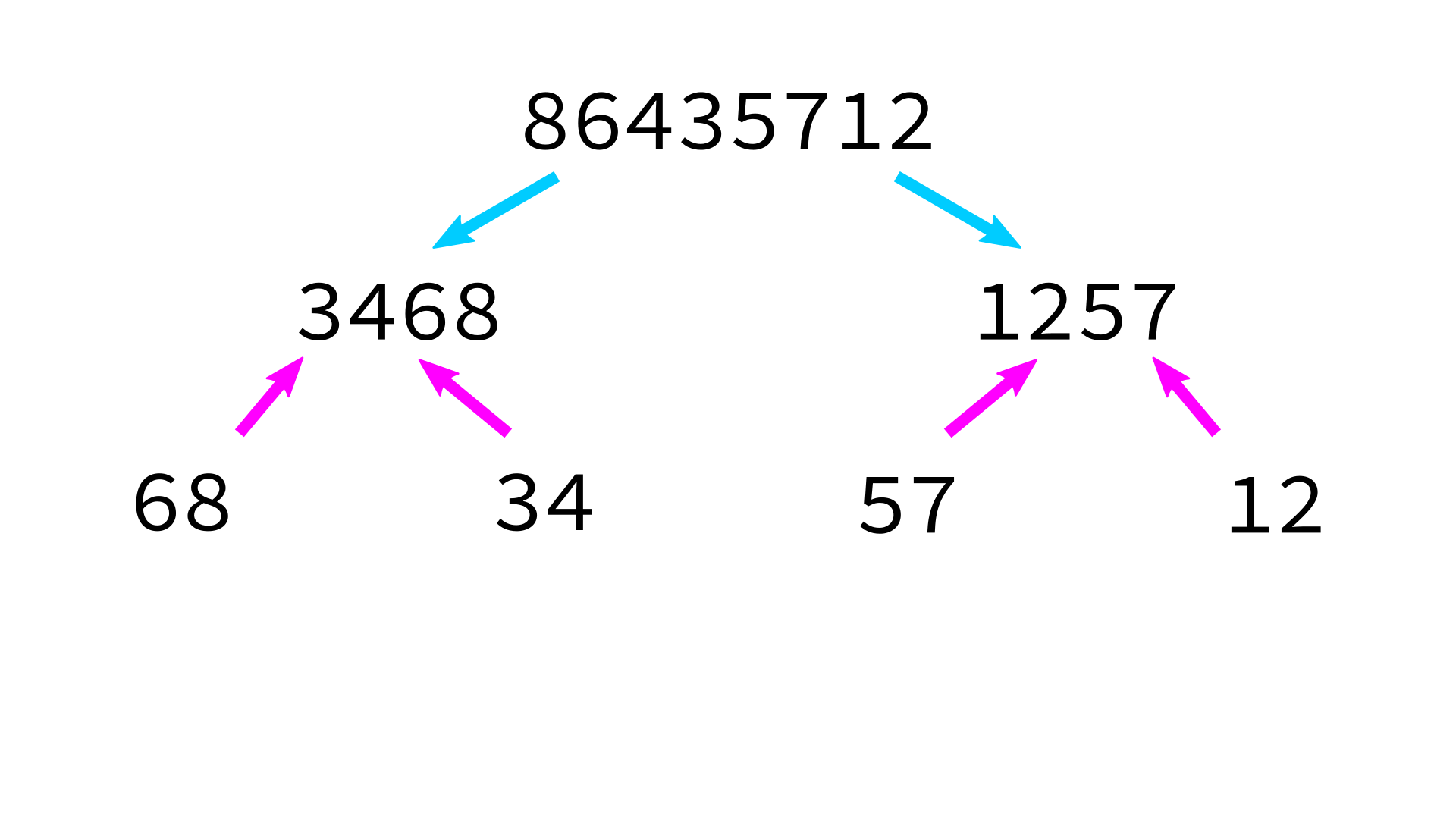
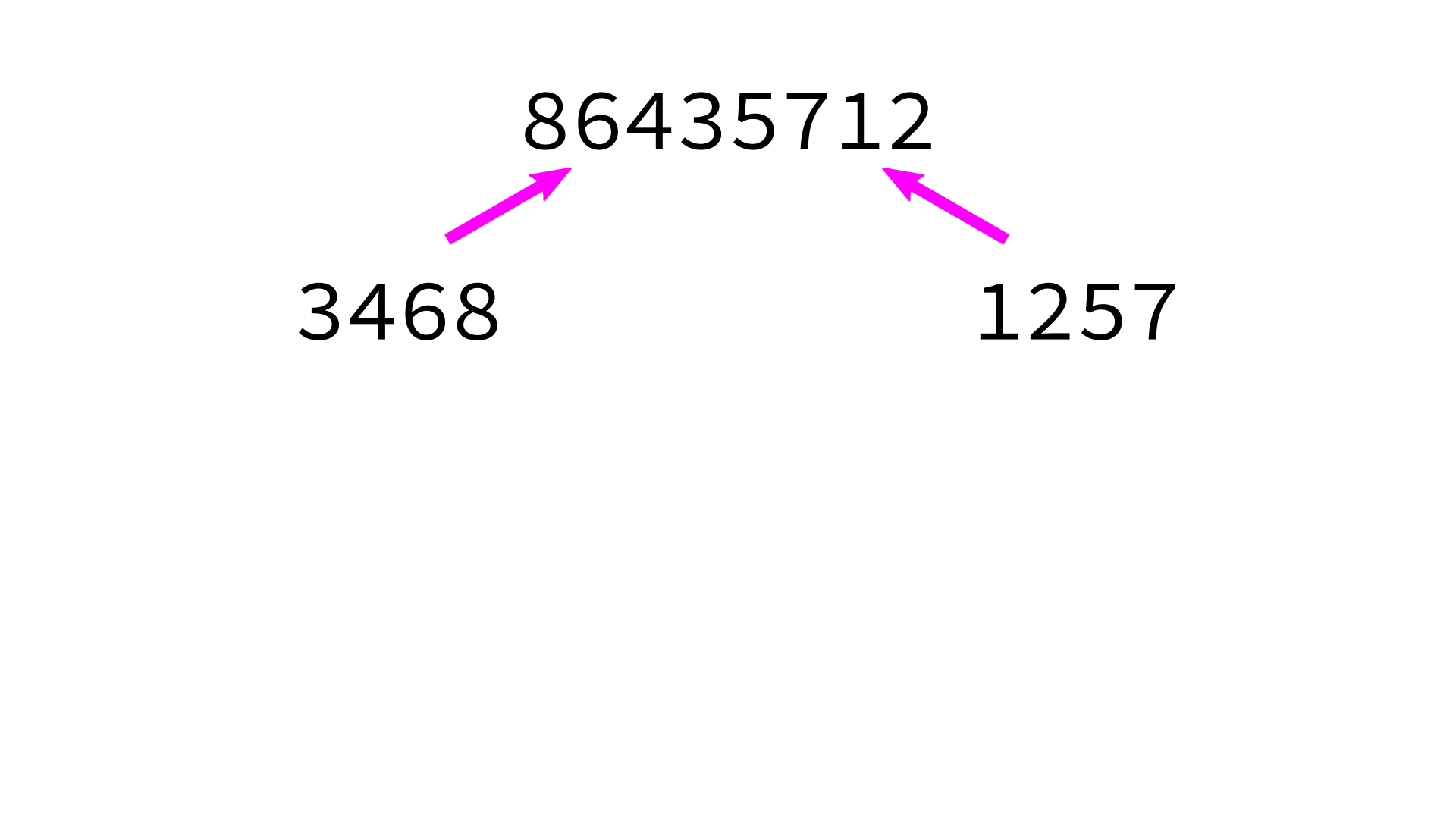
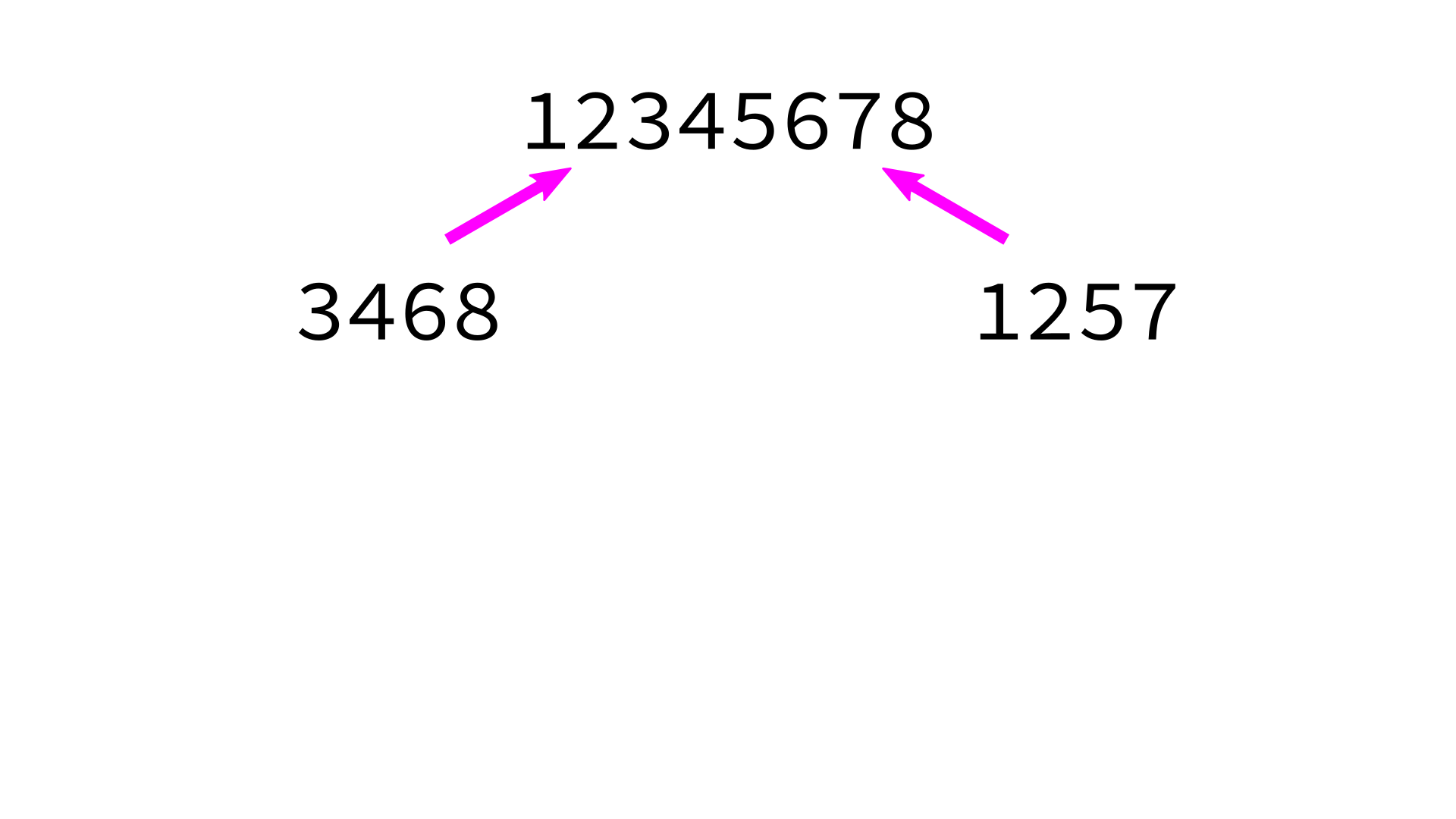

But how to merge?
This algorithm depends on having a function merge_sorted_lists that can merge to sorted lists into a single sorted list.
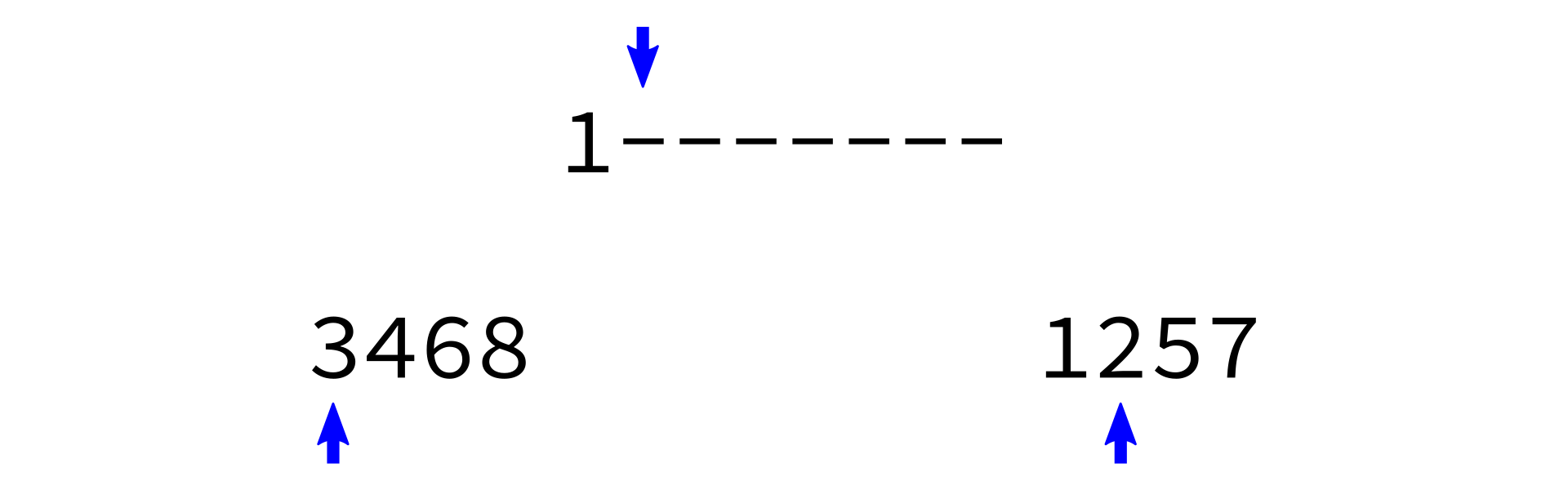
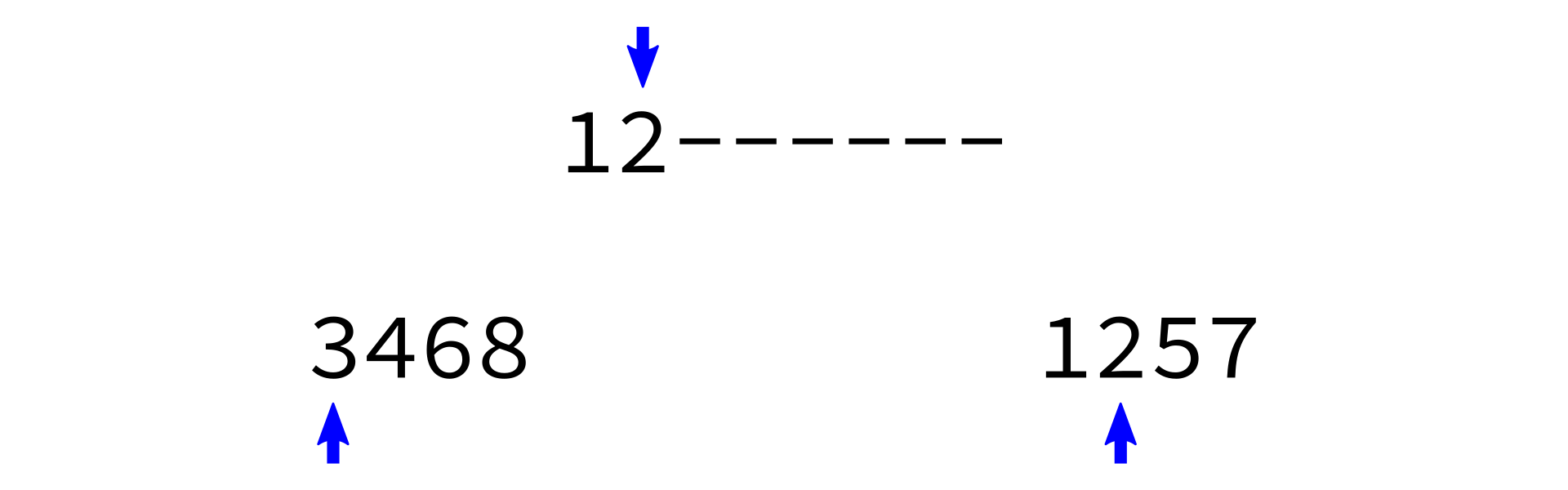
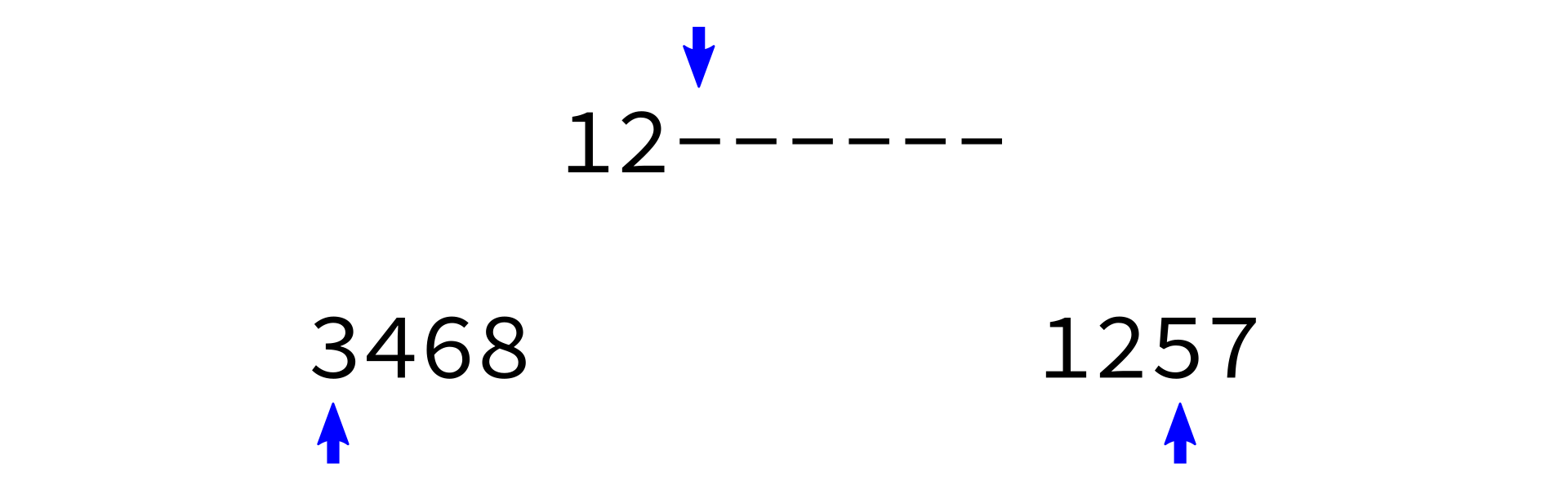
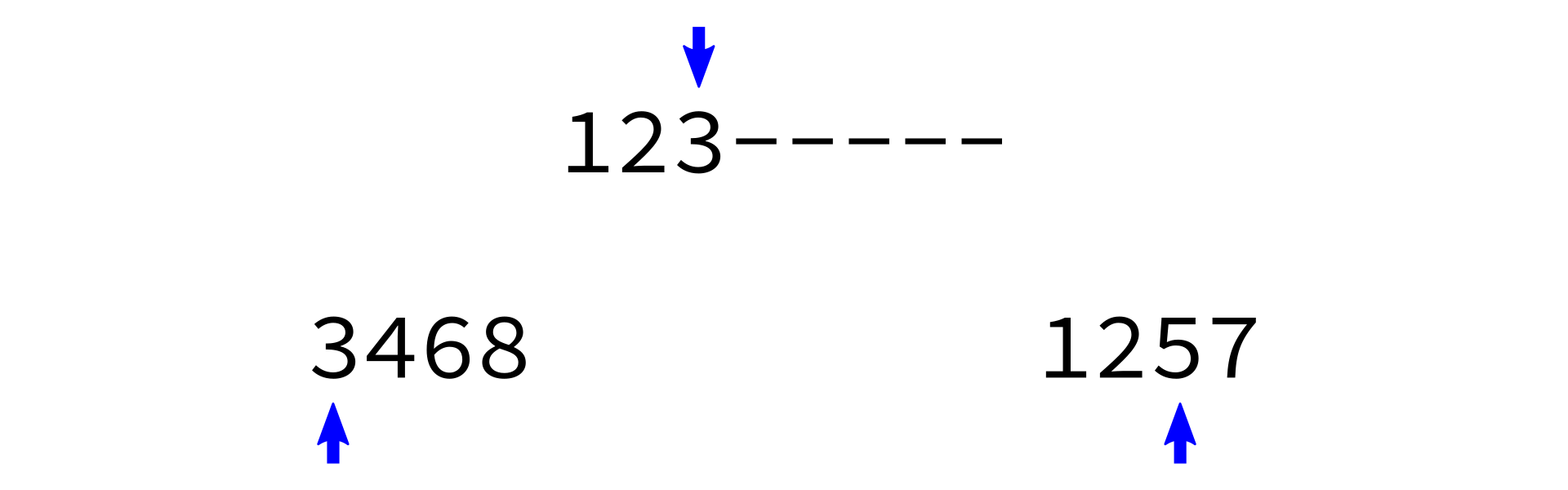
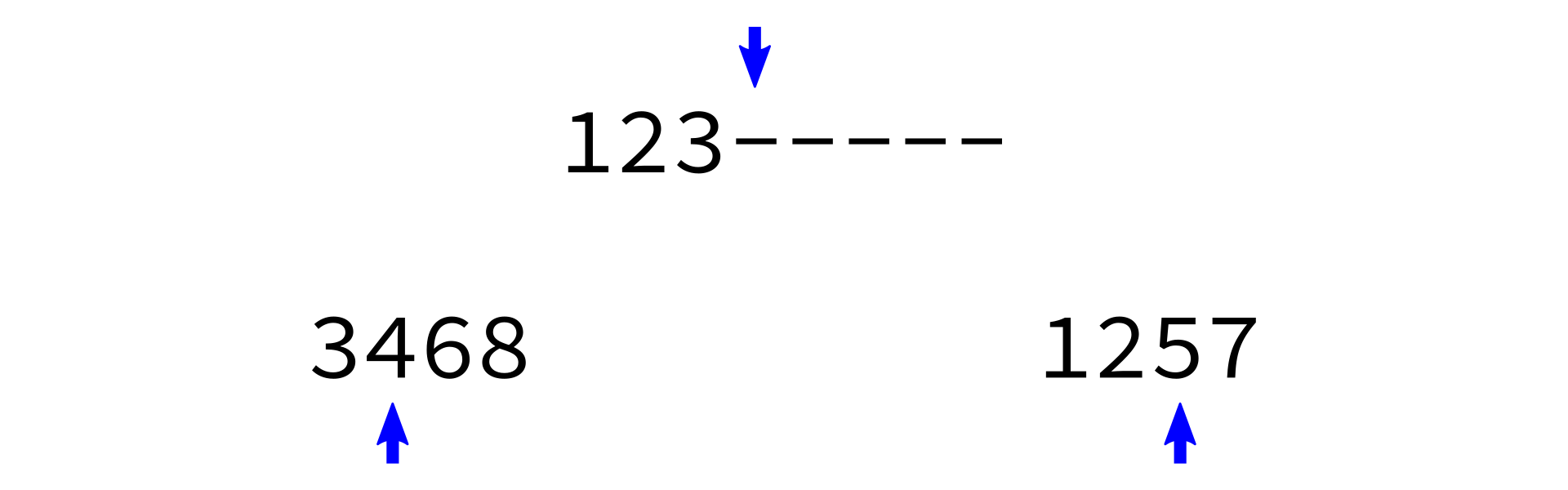
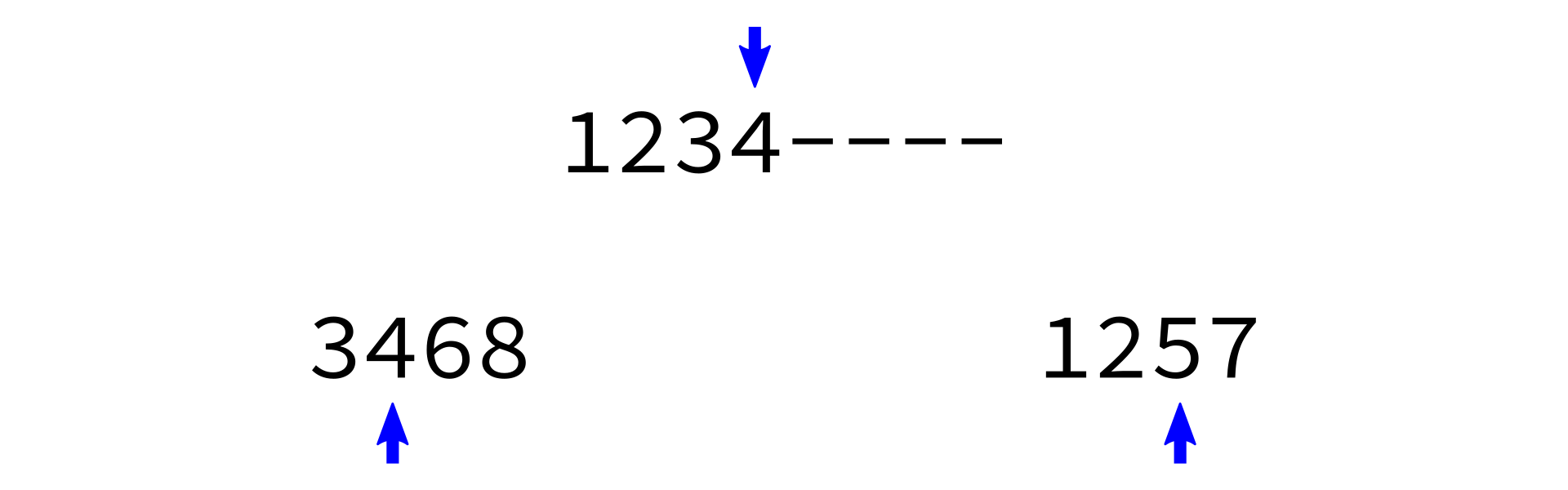
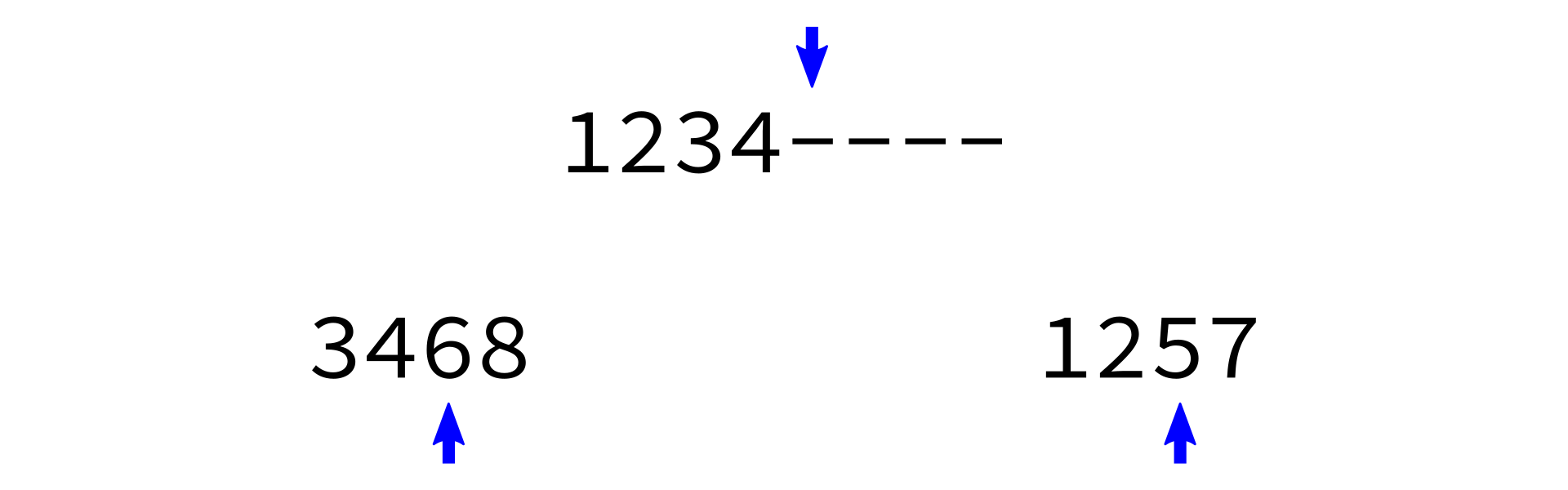
merge_sorted_lists:
Input: sorted lists L1 and L2, and a list L of the proper length in which to store the results.
Goal: copy all elements of L1 and L2 into L in increasing order.
- Make three integer variables
i1,i2,ito keep track of current position inL1,L2,Lrespectively. Set all to zero. - While
i1 < len(L1)andi2 < len(L2), do the following:- Check which of
L1[i1]andL2[i2]is smaller. - Store the smaller one in
L[i]. - Increment whichever one of
i1,i2was used. - Increment
i
- Check which of
- Copy any remaining portion of
L1intoL. - Copy any remaining portion of
L2intoL.
Merging sorted lists



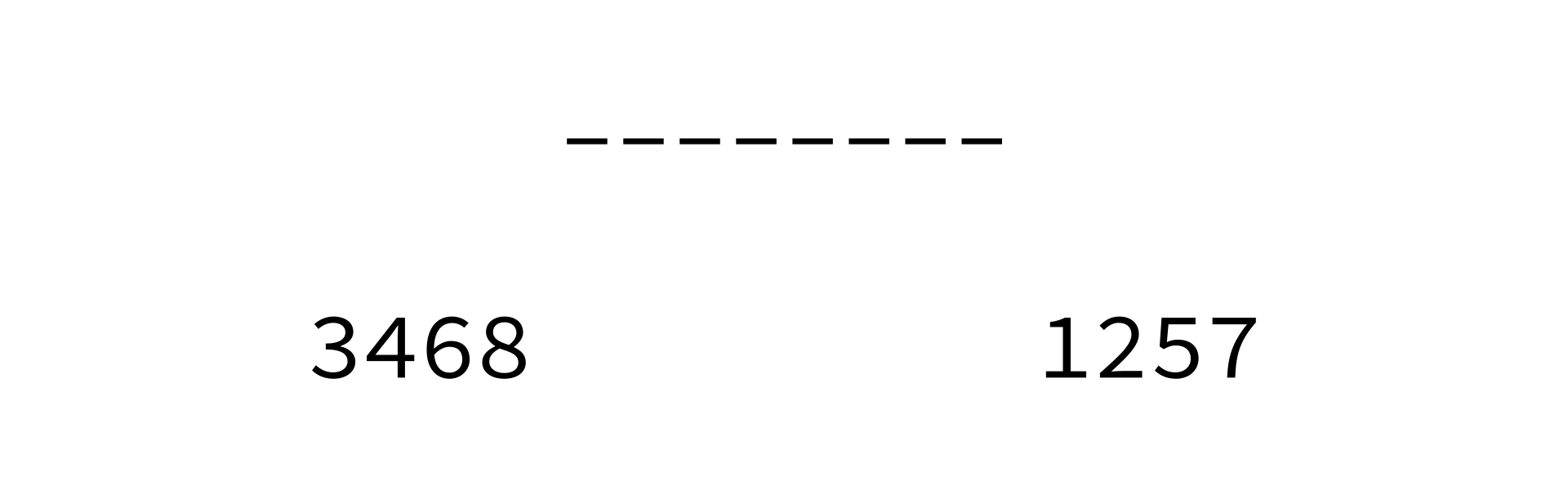
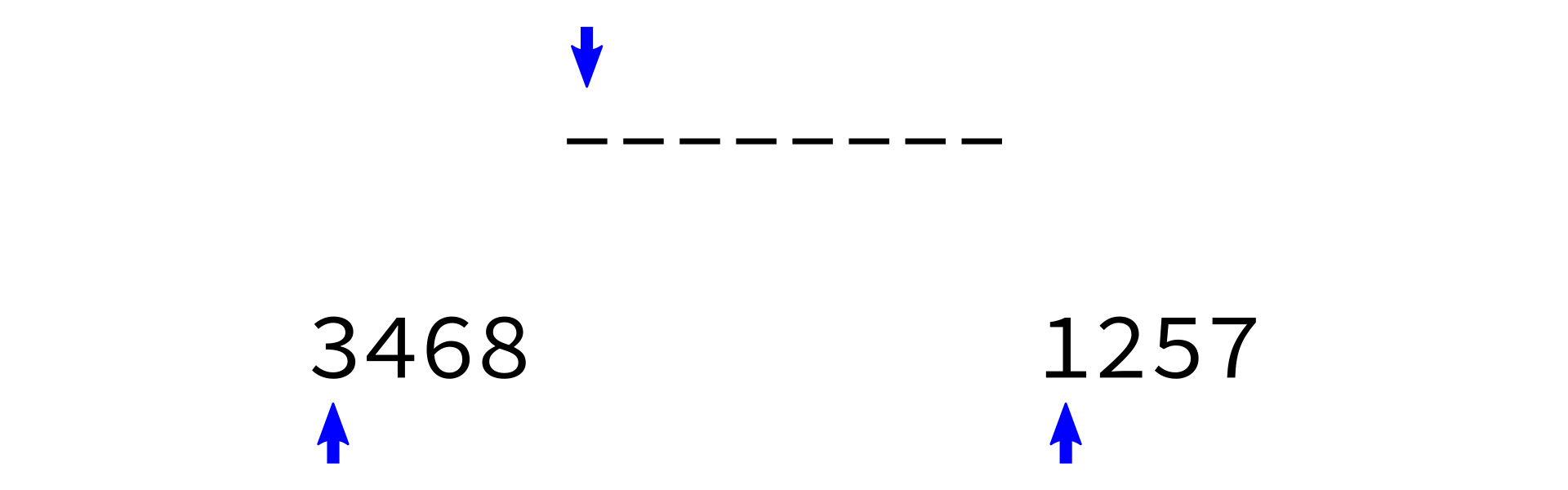
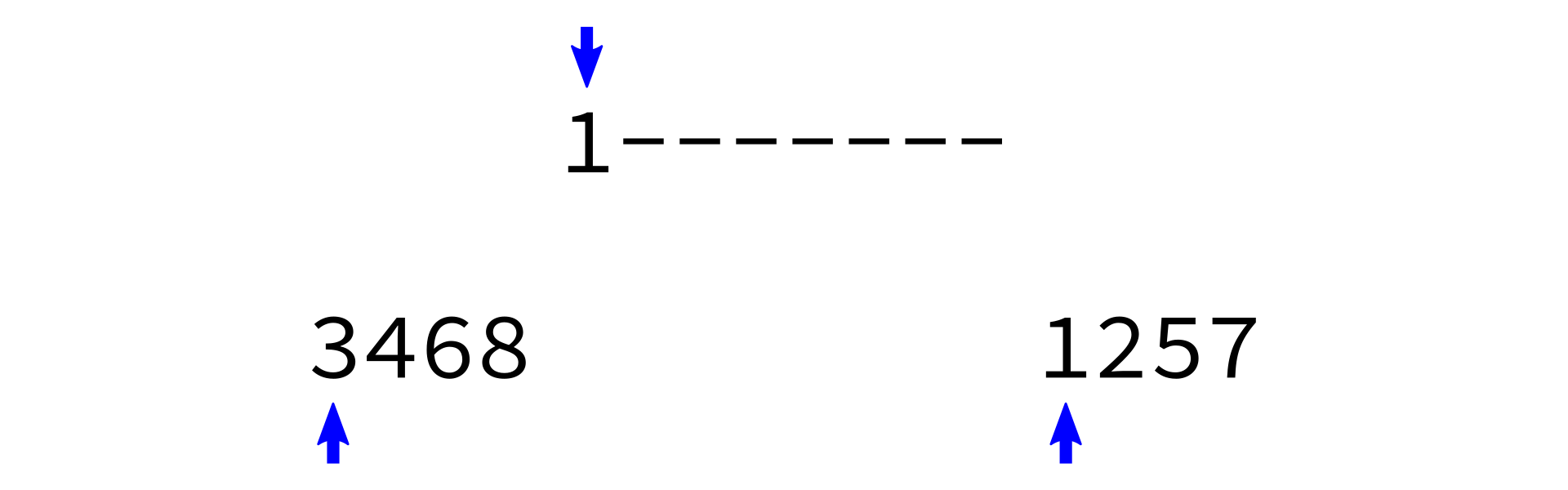
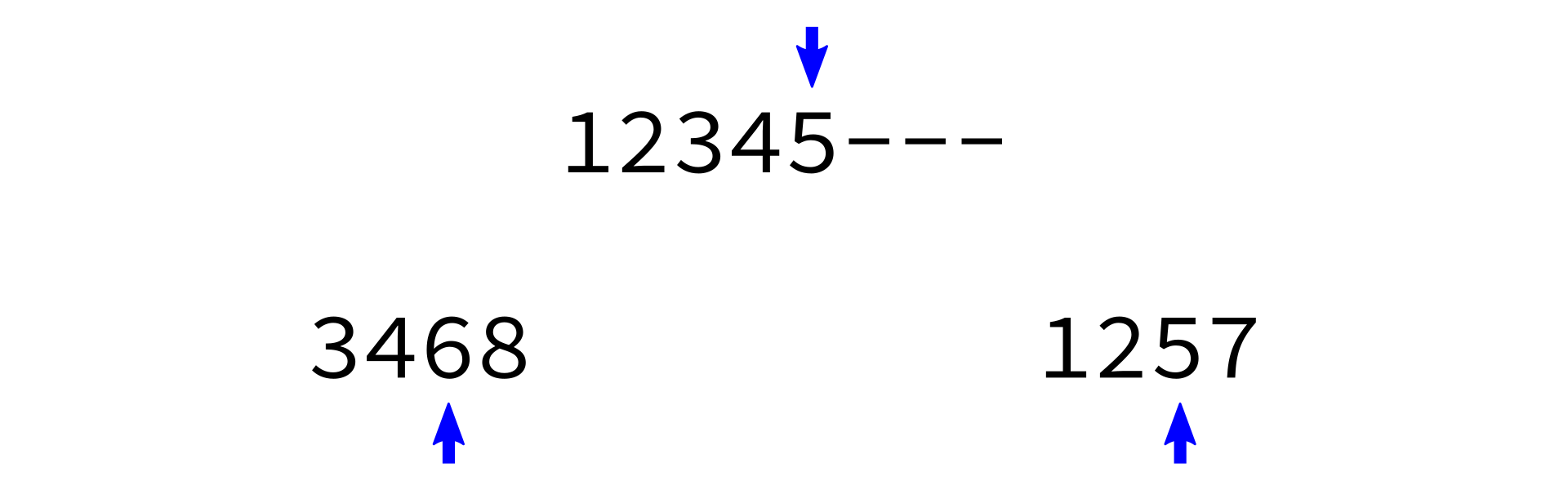









Coding time
Let's implement mergesort in Python.
References
No changes to the references from Lecture 13
- Algorithms by Jeff Erickson, Chapter 1. Mergesort is example 1.4.
- Lutz discusses recursive functions in Chapter 19 (pages 555-559 in the print edition).
- Intro to Python for Computer Science and Data Science by Deitel and Deitel, Chapter 11.
- Think Python, 2ed, by Allen B. Downey, Sections 5.8 to 5.10.
- Computer Science: An Overview by Brookshear and Brylow, Section 5.5.
Revision history
- 2021-02-18 Move unused slides to Lecture 17
- 2021-02-17 Initial publication