Lecture 14
Recursion vs Iteration II
MCS 275 Spring 2021
Emily Dumas
Lecture 14: Recursion vs Iteration II
Course bulletins:
- Project 2 description available.
- Project 2 due 6pm CST Friday, February 26.
- Check out the recursion sample code.
Plan
- A bit about project 2
- More on recursion, iteration, counting function calls
- Start on backtracking
Project 2 topic
Focuses on recursion. Based on special classes of strings that have the "pattern" ABB:
- Egg:
AandBare single characters, e.g.egg,off,aaa - Superegg:
Ais a superegg or single character andBis a single character, e.g.add,addee - Hyperegg:
AandBare each hypereggs or single characters, e.g.anoonoo,offeggegg,gooss
Project 2 task
You'll write functions to test whether a string belongs to these classes.
Details in the project description.
Later I will provide test data, but you'll need to write your own test code.
Fibonacci timing
| n=35 | |
|---|---|
| recursive | 1.9s |
| iterative | <0.001s |
Measured on a 4.00Ghz Intel i7-6700K CPU (2015 release date) with Python 3.8.5
fib call graph
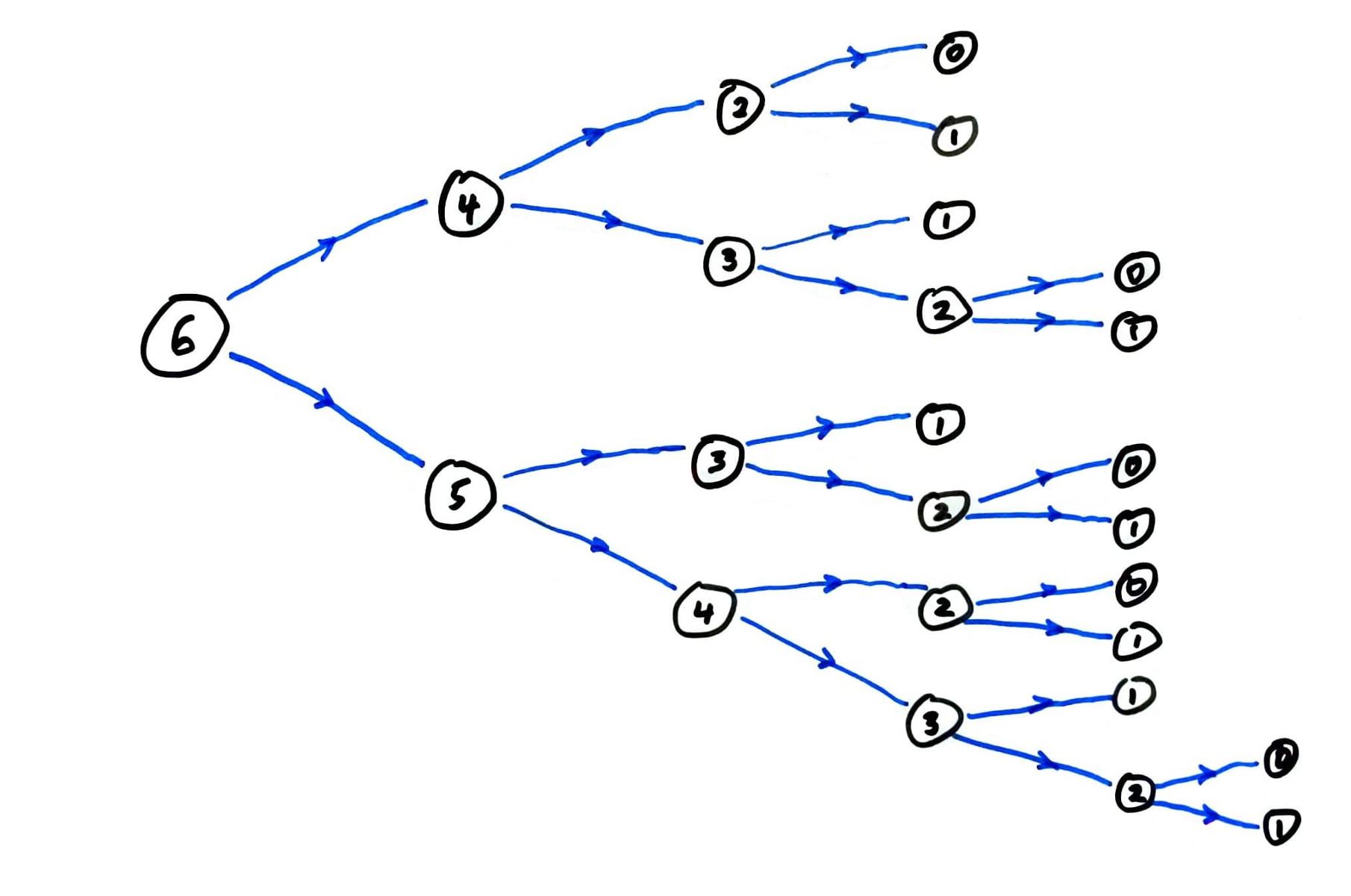
Most Fibonacci numbers are computed many times!
fib call graph
Most Fibonacci numbers are computed many times!
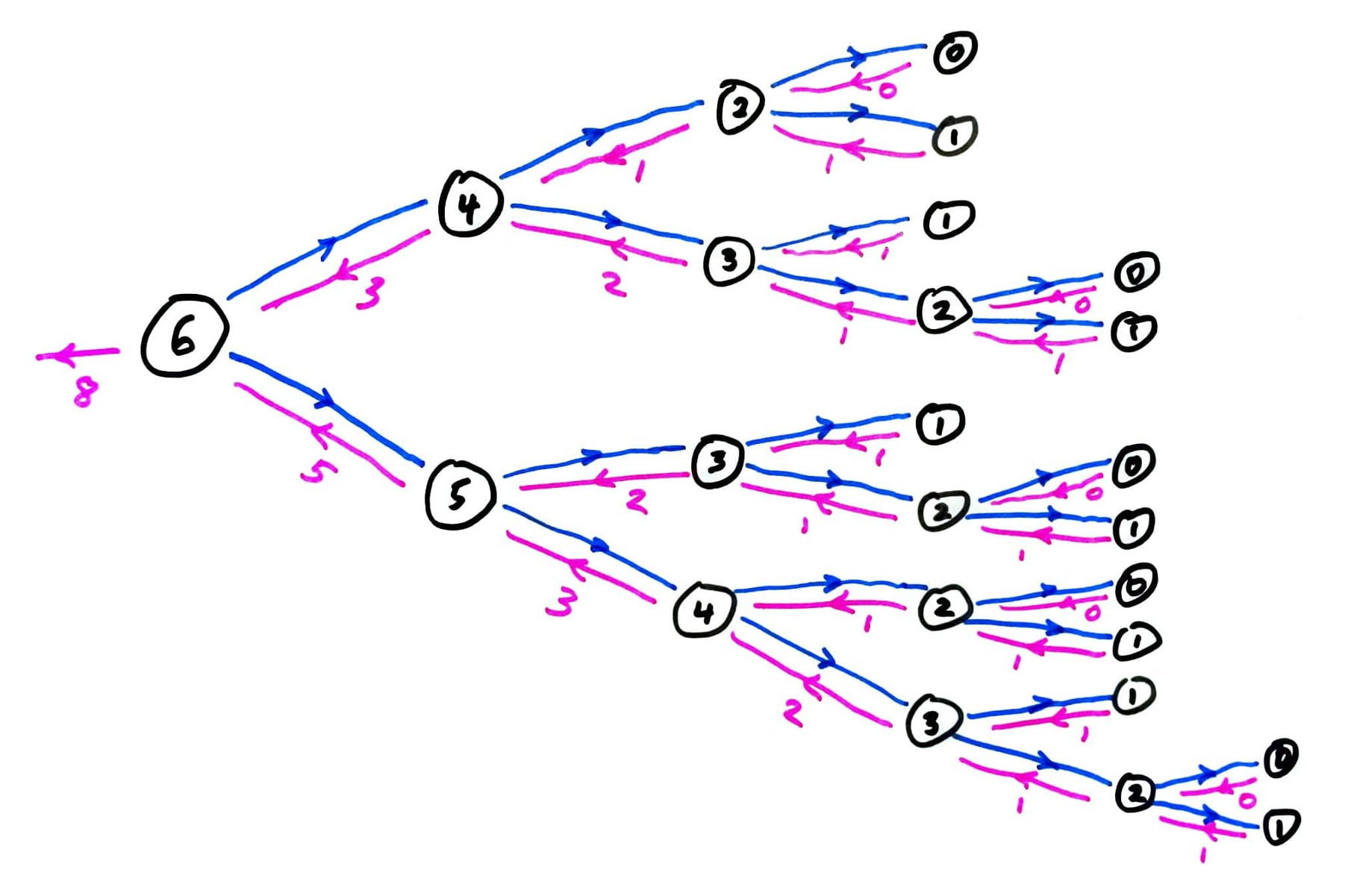
Memoization
fib computes the same terms over and over again.
Instead, let's store all previously computed results, and use the stored ones whenever possible.
This is called memoization. It only works for pure functions, i.e. those which always produce the same return value for any given argument values.
math.sin(...) is pure; time.time() is not.
Memoizing fib
Let's add a simple memoization feature to our recursive fib function.
memoized fib call graph
memoized fib call graph
Fibonacci timing summary
| n=35 | n=450 | |
|---|---|---|
| recursive | 1.9s | > age of universe |
| memoized recursive | <0.001s | 0.003s |
| iterative | <0.001s | 0.001s |
Measured on a 4.00Ghz Intel i7-6700K CPU (2015 release date) with Python 3.8.5
Memoization summary
Recursive functions with multiple self-calls often benefit from memoization.
Memoized version is conceptually similar to an iterative solution.
Memoization does not alleviate recursion depth limits.
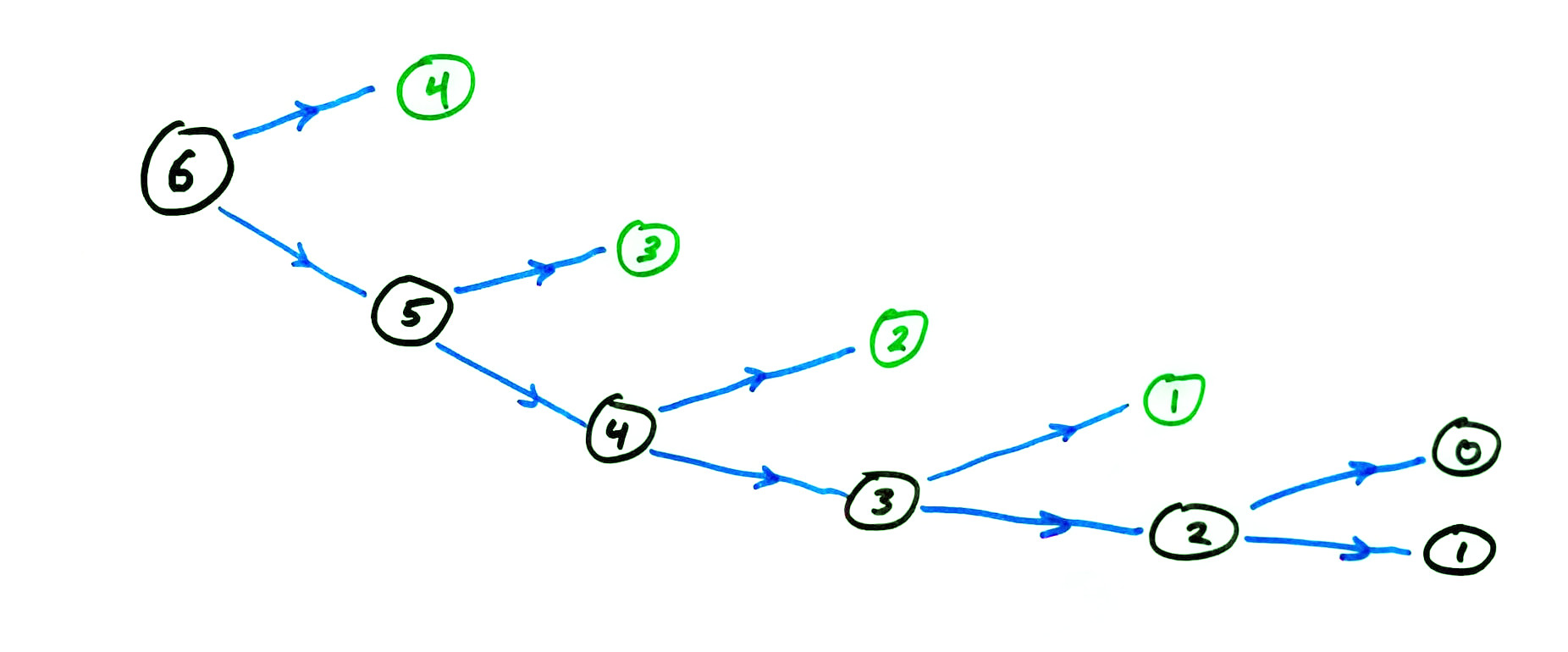
Call counts
One way to measure the expense of a recursive function is to count how many times the function is called.
Let's do this for recursive fib.
| $n$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|---|
| calls | 1 | 1 | 3 | 5 | 9 | 15 | 25 | |
| $F_n$ | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 |
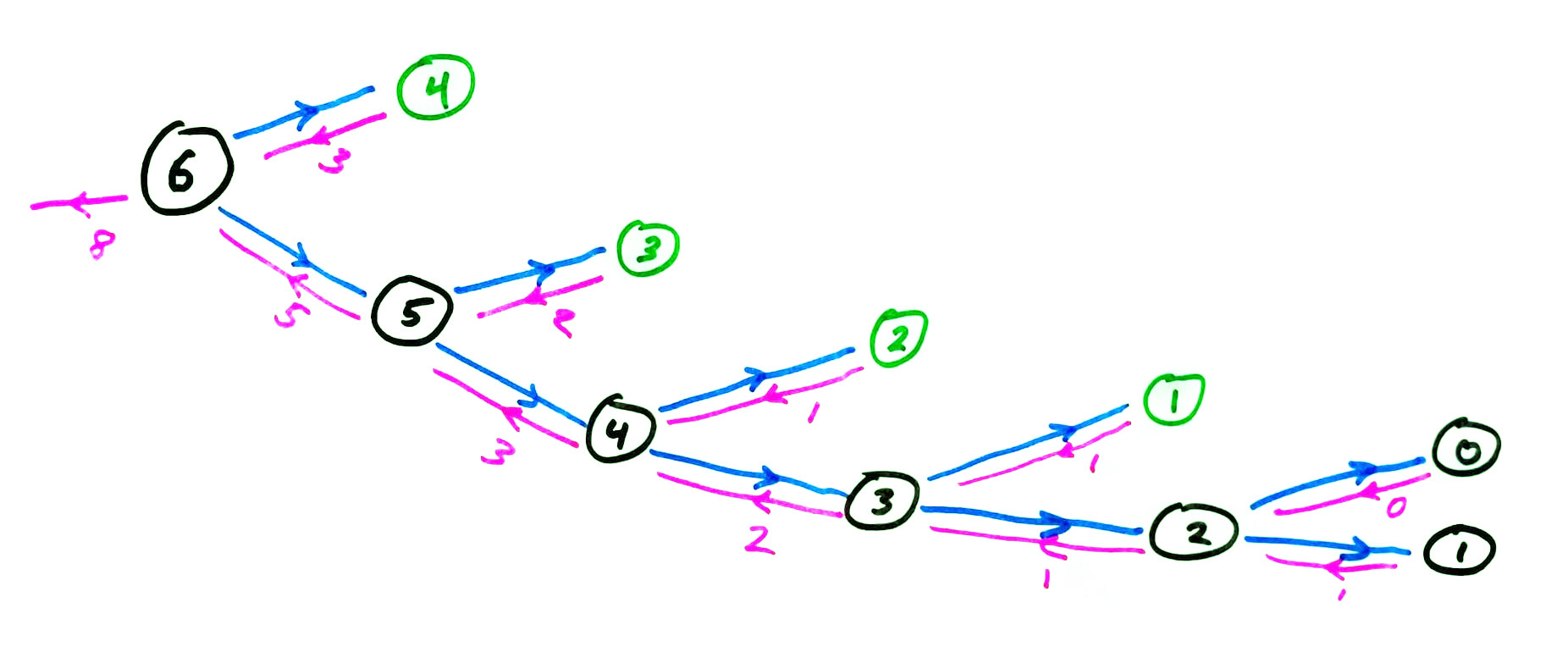
fib is called to compute fib(n). Then
$$T(0)=T(1)=1$$ and $$T(n) = T(n-1) + T(n-2) + 1.$$
Corollary: $T(n) = 2F_{n+1}-1$.
Proof of corollary: Let $S(n) = 2F_{n+1}-1$. Then $S(0)=S(1)=1$, and $$\begin{split}S(n) &= 2F_{n+1}-1 = 2(F_{n} + F_{n-1}) - 1\\ &= (2 F_n - 1) + (2 F_{n-1}-1) + 1\\ & = S(n-1) + S(n-2) + 1\end{split}$$ Therefore $S$ and $T$ have the same first two terms, and follow the same recursive definition based on the two previous terms.
Corollary: Every time we increase $n$ by 1, the naive recursive fib does $\approx61.8\%$ more work.
(The ratio $F_{n+1}/F_n$ approaches $\frac{1 + \sqrt{5}}{2} \approx 1.61803$.)
Recursion with backtracking

How do you solve a maze?
Recursion with backtracking

How do you solve a maze?
References
No changes to the references from Lecture 13
- Algorithms by Jeff Erickson, Chapter 1.
- Lutz discusses recursive functions in Chapter 19 (pages 555-559 in the print edition).
- Intro to Python for Computer Science and Data Science by Deitel and Deitel, Chapter 11.
- Think Python, 2ed, by Allen B. Downey, Sections 5.8 to 5.10.
- Computer Science: An Overview by Brookshear and Brylow, Section 5.5.
Revision history
- 2021-02-15 Move some unused slides over to Lecture 15
- 2021-02-12 Initial publication