Lecture 7
strings and integers
MCS 260 Fall 2021
Emily Dumas
Reminders
- Worksheet 3 available
- Project 1 description posted
Bytes
We've discussed the bit (b) or binary digit (0 or 1). A byte (B) is a sequence of 8 bits, equivalently, an 8-digit binary number or a 2-digit hex number. It can represent an integer between 0=$\texttt{0x00}$ and 255=$\texttt{0xff}$. Computers store information as sequences of bytes.Unicode
Basic problem: How to turn written language into a sequence of bytes?
Unicode (1991) splits this into two steps:
- Make a central directory of characters of most written languages; these are code points
- Specify ways to encode code points into sequences of bytes (not discussed today)
Every code point has a number (an integer between 0 and 0x10ffff=1,114,111).
Code point numbers are always written $\texttt{U+}$ followed by hexadecimal digits.
| $\texttt{U+41}$ | A |
| $\texttt{U+109}$ | ĉ |
| $\texttt{U+1f612}$ | 😒 |
strings
In Python 3, a str is a sequence of code points.
Several syntaxes are supported for literals:
'Hello world' # single quotes
"Hello world" # double quotes
# multi-line string with triple single quote
'''This is a string
that contains line breaks'''
# multi-line string with triple double quote
"""François: How is MCS 260?
Binali: It's going ok. Too many slides.
François: ¯\_(ツ)_/¯"""
Escape sequences
The $\texttt{\\}$ character has special meaning; it begins an escape sequence, such as:- $\texttt{\\n}$ - the newline character
- $\texttt{\\'}$ - a single quote
- $\texttt{\\"}$ - a double quote
- $\texttt{\\\\}$ - a backslash
- $\texttt{\\u0107}$ - Code point $\texttt{U+107}$
- $\texttt{\\U0001f612}$ - Code point $\texttt{U+1f612}$
(There is a full list of escape sequences.)
Note $\texttt{\\}$ appears a lot in Windows paths!
>>> print("I \"like\":\n\u0050\u0079\u0074\u0068\u006f\u006e")
I "like":
Python
>>>
Operations on strings
Most arithmetic operations forbid strings. Exceptions:
- $\texttt{+}$ joins strings, e.g.
"cat"+"erpillar" - $\texttt{*}$ joins a specified number of copies, e.g.
"doo"*6
>>> "Hello" + " " + "world!"
'Hello world!'
>>> "Hello" - "llo"
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: unsupported operand type(s) for -: 'str' and 'str'
>>> "Ha" * 4
'HaHaHaHa'
>>> prefix = "Dr. "
>>> fullname = "Ramanujan"
>>> prefix+fullname
'Dr. Ramanujan'
sequence stuff
Reminder: Like lists, strings are sequences.
You can use indexing to get individual characters, slices to get substrings, and len(...) to get the length.
str
Python's str() function converts any other value to a string, e.g.
>>> str(5678)
'5678'
>>> str(5678)[1]
'6'
>>> int(str(5678)[1])
6
str() is rarely needed, but it does give a way to access decimal digits of an integer individually.
int
When converting from a string, $\texttt{int()}$ defaults to base $10$. But it supports other bases as well. The base is given as the second argument of the function.
>>> int("1001",2)
9
>>> int("3e",16)
62
>>> int("0b1001",0)
9
>>> int("0x3e",0)
62
>>> int("77",0)
77
Bitwise operators
There are certain operators that only work on ints, and which are based on the bits in the binary expression:
| $\texttt{<<}$ | $\texttt{>>}$ | $\texttt{&}$ | $\texttt{|}$ | $\texttt{^}$ |
| left shift | right shift | bitwise AND | bitwise OR | bitwise XOR |
$\texttt{a << b}$ moves the bits of $\texttt{a}$ left by $\texttt{b}$ positions.
$\texttt{a >> b}$ moves the bits of $\texttt{a}$ right by $\texttt{b}$ positions.
(This detroys the lowest $\texttt{b}$ bits of $\texttt{a}$.)
>>> 9 << 3 # 9 = 0b1001 becomes 0b1001000 = 72
72
>>> 7 << 1 # 7 = 0b111 becomes 0b1110 = 14
14
>>> 9 >> 2 # 9 = 0b1001 becomes 0b10
2
>>> 9 & 5 # 9 = 0b1001, 5 = 0b0101
1
| 1 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 1 | |
| AND: | 0 | 0 | 0 | 1 |
>>> 9 | 5 # 9 = 0b1001, 5 = 0b0101
13
| 1 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 1 | |
| OR: | 1 | 1 | 0 | 1 |
>>> 9 ^ 5 # 9 = 0b1001, 5 = 0b0101
12
| 1 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 1 | |
| XOR: | 1 | 1 | 0 | 0 |
Logic gates
Circuits that perform logic operations on bits, logic gates, are fundamental building blocks of computers.
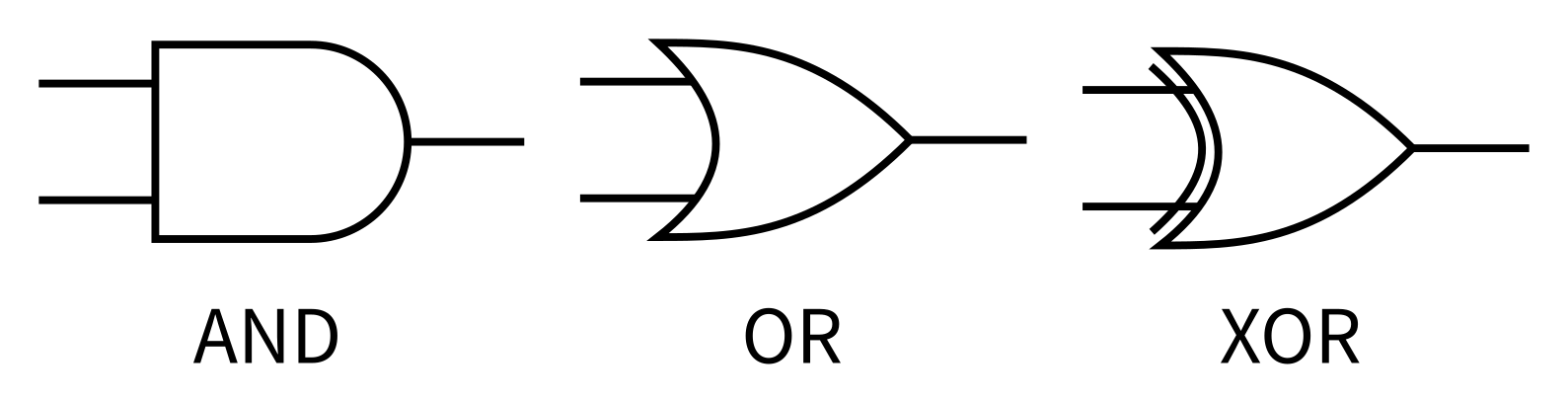
Thus the Python operators $\texttt{<<}$,$\texttt{>>}$,$\texttt{&}$,$\texttt{|}$,$\texttt{^}$ are especially low-level operations.

This chip (or integrated circuit / IC) contains four AND gates built from about $50$ transistors. The processor in an iPhone 11 has about $8,\!500,\!000,\!000$ transistors.
References
- Official Unicode code point charts
- In Downey: Strings are discussed in Section 2.6 and Chapter 8
- Bitwise operations in the Python 3 documentation
- The int() feature of converting from strings in other bases is also discussed in the Python 3 documentation.
- Bitwise operations and logic gates are discussed in sections 1.1 and 2.4 of Brookshear & Brylow.
Revision history
- 2021-09-08 Initial publication
- 2021-09-09 Fix typo