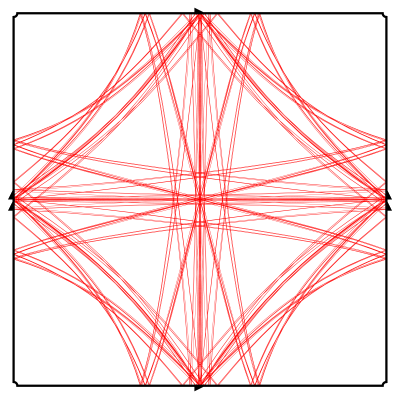
The left image above shows an approximation of a Birman-Series set consisting of the 88 shortest geodesics on a hyperbolic punctured torus. Because a long simple geodesic can be approximated in C1 by arcs from closed geodesics of moderate length, this finite union of closed geodesics is a reasonable approximation of the full set.
The underlying Riemann surface in this example is the one obtained by identifying opposite sides of the unit square and removing the point corresponding to the four corners. A conformal mapping from a fundamental domain for the corresponding Fuchsian group is used to map the geodesics to the unit square.
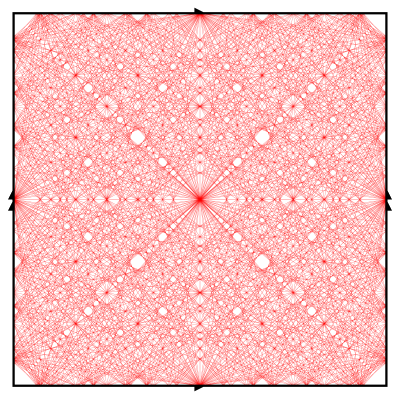
The right image above shows the same collection of homology classes of closed geodesics on the square Euclidean torus. In contrast to the sparseness of the hyperbolic case, here the simple closed geodesics are dense in the unit tangent bundle. While a homology class does not uniquely determine a closed geodesic in the Euclidean case, in this image each representatives is chosen to pass through the same set of Weierstrass points as the corresponding hyperbolic geodesic.
These images were originally created for a poster session at the workshop "Aspects of hyperbolicity in geometry, topology, and dynamics" at the University of Warwick (celebrating Caroline Series' 60th birthday), July 25-27, 2011. The versions appearing in the final poster use slightly different color, line width, and transparency settings.